题目内容
(本小题满分10分)已知二次函数f (x) = x2 – 16x + p + 3.
(1)若函数在区间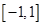 上存在零点,求实数p的取值范围;
上存在零点,求实数p的取值范围;
(2)问是否存在常数q(q≥0),当x∈[q,10]时, 的值域为区间
的值域为区间 ,且
,且 的长度为
的长度为
12 – q.(注:区间[a,b](a<b)的长度为b – a)
(1)若函数在区间
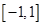 上存在零点,求实数p的取值范围;
上存在零点,求实数p的取值范围;(2)问是否存在常数q(q≥0),当x∈[q,10]时,
 的值域为区间
的值域为区间 ,且
,且 的长度为
的长度为12 – q.(注:区间[a,b](a<b)的长度为b – a)
(1)–20≤p≤12;(2)存在常数q = 8或q = 9,当x∈[q,10]时, 的值域为区间
的值域为区间 ,且
,且 的长度为12–q.
的长度为12–q.
 的值域为区间
的值域为区间 ,且
,且 的长度为12–q.
的长度为12–q.(1)利用零点存在性定理列出关于q的不等式,然后再利用不等式知识求解即可;(2)先利用单调性求出函数的值域,再利用区间长度列出关于q的方程,求解即可。
解:(1)∵二次函数f (x)= x2 – 16x + p + 3的对称轴是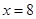 ,∴函数
,∴函数 在区间
在区间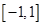 上单调递减,则函数
上单调递减,则函数 在区间
在区间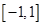 上存在零点须满足
上存在零点须满足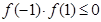 . ……………2分
. ……………2分
即(1 + 16 + p + 3)(1 – 16 + p + 3)≤0, 解得–20≤p≤12. …………………4分
⑵ 当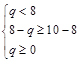 时,即0≤q≤6时,
时,即0≤q≤6时,
 的值域为:[f (8),f (q)],即[p–61, q2 –16q + p + 3].
的值域为:[f (8),f (q)],即[p–61, q2 –16q + p + 3].
∴区间长度为q2 – 16q + p + 3 – (p – 61) = q2 – 16q + 64 =" 12" – q.
∴q2 – 15q + 52 =" 0" ∴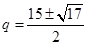 ,经检验
,经检验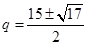 不合题意,舍去.……6分
不合题意,舍去.……6分
当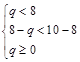 时,即6≤q<8时,
时,即6≤q<8时, 的值域为:
的值域为: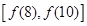 ,即[p – 61,p – 57]
,即[p – 61,p – 57]
∴区间长度为p – 57 – (p – 61) =" 4" =" 12" – q ∴q = 8.经检验q = 8不合题意,舍去. …8分
当q≥8时, 的值域为:[f (q),f (10)],即 [q2 – 16q + p +3,p – 57].
的值域为:[f (q),f (10)],即 [q2 – 16q + p +3,p – 57].
∴区间长度为p – 57 –(q2 – 16q + p + 3) = –q2 – 16q – 60 =" 12" – q,
∴q2 – 17q + 72 =" 0" , ∴q = 8或q = 9.经检验q = 8或q = 9满足题意.
所以存在常数q = 8或q = 9,当x∈[q,10]时, 的值域为区间
的值域为区间 ,且
,且 的长度为12–q. ………………………10分
的长度为12–q. ………………………10分
解:(1)∵二次函数f (x)= x2 – 16x + p + 3的对称轴是
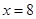 ,∴函数
,∴函数 在区间
在区间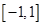 上单调递减,则函数
上单调递减,则函数 在区间
在区间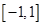 上存在零点须满足
上存在零点须满足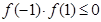 . ……………2分
. ……………2分即(1 + 16 + p + 3)(1 – 16 + p + 3)≤0, 解得–20≤p≤12. …………………4分
⑵ 当
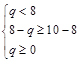 时,即0≤q≤6时,
时,即0≤q≤6时, 的值域为:[f (8),f (q)],即[p–61, q2 –16q + p + 3].
的值域为:[f (8),f (q)],即[p–61, q2 –16q + p + 3].∴区间长度为q2 – 16q + p + 3 – (p – 61) = q2 – 16q + 64 =" 12" – q.
∴q2 – 15q + 52 =" 0" ∴
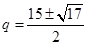 ,经检验
,经检验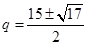 不合题意,舍去.……6分
不合题意,舍去.……6分当
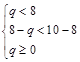 时,即6≤q<8时,
时,即6≤q<8时, 的值域为:
的值域为: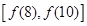 ,即[p – 61,p – 57]
,即[p – 61,p – 57]∴区间长度为p – 57 – (p – 61) =" 4" =" 12" – q ∴q = 8.经检验q = 8不合题意,舍去. …8分
当q≥8时,
 的值域为:[f (q),f (10)],即 [q2 – 16q + p +3,p – 57].
的值域为:[f (q),f (10)],即 [q2 – 16q + p +3,p – 57].∴区间长度为p – 57 –(q2 – 16q + p + 3) = –q2 – 16q – 60 =" 12" – q,
∴q2 – 17q + 72 =" 0" , ∴q = 8或q = 9.经检验q = 8或q = 9满足题意.
所以存在常数q = 8或q = 9,当x∈[q,10]时,
 的值域为区间
的值域为区间 ,且
,且 的长度为12–q. ………………………10分
的长度为12–q. ………………………10分
练习册系列答案
相关题目

 在区间
在区间 上的最大值和最小值,(
上的最大值和最小值,( 是自然对数的底数),
是自然对数的底数), 上,函数
上,函数 的图像的下方。
的图像的下方。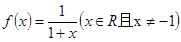

 和
和 的值
的值 (2)
(2) 的值,并求
的值,并求 的解析式。
的解析式。 .
.  时,求函数
时,求函数 的定义域;
的定义域; 的不等式
的不等式 的解集是
的解集是 ,求
,求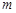 的取值范围.
的取值范围.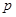 万元和
万元和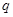 万元,它们与投入资金万元的关系为:
万元,它们与投入资金万元的关系为: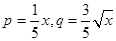 今有3万元资金投入经营这两种商品,为获得最大利润,对这两种商品的资金分别投入多少时,能获得最大利润?最大利润是多少?
今有3万元资金投入经营这两种商品,为获得最大利润,对这两种商品的资金分别投入多少时,能获得最大利润?最大利润是多少? ,具有性质:
,具有性质: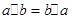 ;②
;②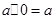 ;③
;③ 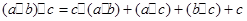 ,
,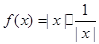 的最小值为 .
的最小值为 .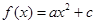 ,且
,且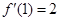 ,则
,则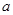 的值为 ( )
的值为 ( ) 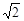
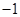
 ,则
,则