题目内容
设函数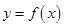 的定义域为
的定义域为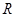 ,则函数
,则函数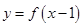 和函数
和函数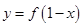 的图象关于( )
的图象关于( )
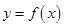 的定义域为
的定义域为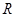 ,则函数
,则函数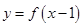 和函数
和函数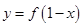 的图象关于( )
的图象关于( )A.直线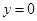 对称 对称 | B.直线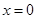 对称 对称 |
C.直线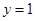 对称 对称 | D.直线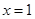 对称 对称 |
D
试题分析:当
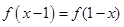 时,x=1,∴函数
时,x=1,∴函数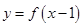 和函数
和函数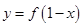 的图象关于直线
的图象关于直线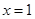 对称,故选D
对称,故选D点评:函数
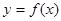 关于
关于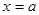 对称
对称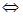
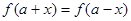 ,掌握此知识点是解决此类问题的关键
,掌握此知识点是解决此类问题的关键
练习册系列答案
 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案
相关题目
题目内容
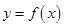 的定义域为
的定义域为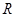 ,则函数
,则函数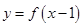 和函数
和函数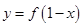 的图象关于( )
的图象关于( )A.直线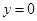 对称 对称 | B.直线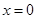 对称 对称 |
C.直线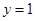 对称 对称 | D.直线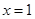 对称 对称 |
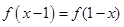 时,x=1,∴函数
时,x=1,∴函数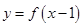 和函数
和函数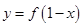 的图象关于直线
的图象关于直线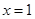 对称,故选D
对称,故选D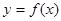 关于
关于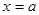 对称
对称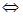
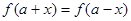 ,掌握此知识点是解决此类问题的关键
,掌握此知识点是解决此类问题的关键
 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案