题目内容
【题目】已知数列![]() 为等比数列,
为等比数列,![]() ,公比为
,公比为![]() ,且
,且![]() ,
,![]() 为数列
为数列![]() 的前
的前![]() 项和.
项和.
(1)若![]() ,求
,求![]() ;
;
(2)若调换![]() 的顺序后能构成一个等差数列,求
的顺序后能构成一个等差数列,求![]() 的所有可能值;
的所有可能值;
(3)是否存在正常数![]() ,使得对任意正整数
,使得对任意正整数![]() ,不等式
,不等式![]() 总成立?若存在,求出
总成立?若存在,求出![]() 的范围,若不存在,请说明理由.
的范围,若不存在,请说明理由.
【答案】(1)![]() ;(2)
;(2)![]() 或
或![]() ;(3)
;(3)![]() .
.
【解析】
(1)运用等比数列的通项公式,解方程可得公比,求和公式计算即可得到所求值;
(2)由等比数列的通项公式和等差数列中项的性质,解方程即可得到所求值;
(3)假设存在正常数c,q,使得对任意的正整数n,不等式![]() 总成立,由
总成立,由![]() ,即为
,即为![]() ,等价为
,等价为![]() ,讨论公比q,结合题意,推得存在,求得q的范围.
,讨论公比q,结合题意,推得存在,求得q的范围.
(1)因为![]() 所以
所以![]() ,所以
,所以![]() 或
或![]() (舍去).
(舍去).
所以![]()
(2)若![]() 或
或![]() 成等差数列,则
成等差数列,则![]() ,解得
,解得![]() 或1(舍去);若
或1(舍去);若![]() 或
或![]() 成等差数列,
成等差数列,
则![]() ,解得
,解得![]() 或1(舍去);若
或1(舍去);若![]() 成等差数列,
成等差数列,
则![]() ,解得
,解得![]() (舍去).综上,
(舍去).综上,![]()
(3)由![]() ,可得
,可得![]() ,故等价于
,故等价于![]() 恒成立.
恒成立.
因为![]()
![]() 所以
所以![]() 得到
得到![]() 当
当![]() 时,
时,![]() 不可能成立.
不可能成立.
当![]() 时,另
时,另![]() ,得
,得![]() ,解得
,解得![]()
因为![]() ,所以
,所以![]() 即当
即当![]() 时,
时,![]() ,所以
,所以![]() 不可能成立.
不可能成立.
当![]() 时,由
时,由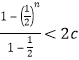 ,即
,即![]() ,所以
,所以![]()
即当![]() 时,
时,![]() 不成立.当
不成立.当![]() 时,
时,![]() ,
,
所以当![]() 时
时![]() 恒成立,
恒成立,
综上,存在正常数![]() ,使得对任意正整数
,使得对任意正整数![]() 不等式
不等式![]() 总成立,
总成立,![]() 的取值范围为
的取值范围为![]()

 阅读快车系列答案
阅读快车系列答案【题目】下面有两个关于“袋子中装有红、白两种颜色的相同小球,从袋中无放回地取球”的游戏规则,这两个游戏规则公平吗?为什么?
游 戏 1 | 游 戏 2 |
2个红球和2个白球 | 3个红球和1个白球 |
取1个球,再取1个球 | 取1个球,再取1个球 |
取出的两个球同色→甲胜 | 取出的两个球同色→甲胜 |
取出的两个球不同色→乙胜 | 取出的两个球不同色→乙胜 |
【题目】为了让学生更多地了解“数学史”知识,某班级举办一次“追寻先哲的足迹,倾听数学的声音的数学史知识竞赛活动.现将初赛答卷成绩(得分均为整数,满分为100分)进行统计,制成如下频率分布表:
序号 | 分数段 | 人数 | 频率 |
1 |
| 10 | 0.20 |
2 |
| ① | 0.44 |
3 |
| ② | ③ |
4 |
| 4 | 0.08 |
合计 | 50 | 1 | |
(1)填充上述表中的空格(在解答中直接写出对应空格序号的答案);
(2)若利用组中值近似计算数据的平均数,求此次数学史初赛的平均成绩;
(3)甲同学的初赛成绩在![]() ,学校为了宣传班级的学习经验,随机抽取分数在
,学校为了宣传班级的学习经验,随机抽取分数在![]() 的4位同学中的两位同学到学校其他班级介绍,求甲同学被抽取到的概率.
的4位同学中的两位同学到学校其他班级介绍,求甲同学被抽取到的概率.