题目内容
【题目】给出下列4个命题,其中正确命题的个数是( )
①计算:9192除以100的余数是1;
②命题“x>0,x﹣lnx>0”的否定是“x>0,x﹣lnx≤0”;
③y=tanax(a>0)在其定义域内是单调函数而且又是奇函数;
④命题p:“|a|+|b|≤1”是命题q:“对任意的x∈R,不等式asinx+bcosx≤1恒成立”的充分不必要条件.
A.1个
B.2个
C.3个
D.4个
【答案】B
【解析】解:①由于9192=(100﹣9)92=C92010092(﹣9)0+…+C92911001(﹣9)91+C92921000(﹣9)92 ,
在此展开式中,除了最后一项外,其余的项都能被100整除,故9192除以100的余数等价于C92921000(﹣9)92=992除以100的余数,而992=(10﹣1)92=C9201092(﹣1)0+…+C9291101(﹣1)91+C9292100(﹣9)92 , 故992除以100的余数等价于C9291101(﹣1)91+C9292100(﹣9)92除以100的余数,而C9291101(﹣1)91+C9292100(﹣9)92=﹣919=﹣10×100+81,故9192除以100的余数是81.不正确.故①错误;
②命题“x>0,x﹣lnx>0”的否定是“x>0,x﹣lnx≤0”,正确;
③y=tanax(a>0)在其定义域内不是单调函数,是奇函数;故③错误,
④当a=b=0时,不等式asinx+bcosx≤1恒成立.
a与b不全为0时,不等式asinx+bcosx≤1化为:sin(x+θ)≤ ![]() ,
,
∵对任意的x∈R,不等式asinx+bcosx≤1恒成立”,
∴ ![]() ≥1,
≥1,
∴a2+b2≤1,画出图象:可知:(a,b)表示的是以原点为圆心,1为半径的圆及其内部.
而|a|+|b|≤1可知:(a,b)表示的是正方形ABCD及其内部.
∴p是q的充分不必要条件.故④正确,
故选:B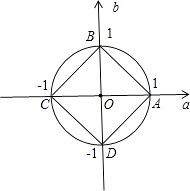
【考点精析】掌握命题的真假判断与应用是解答本题的根本,需要知道两个命题互为逆否命题,它们有相同的真假性;两个命题为互逆命题或互否命题,它们的真假性没有关系.

 计算高手系列答案
计算高手系列答案【题目】为了让学生更多地了解“数学史”知识,某班级举办一次“追寻先哲的足迹,倾听数学的声音的数学史知识竞赛活动.现将初赛答卷成绩(得分均为整数,满分为100分)进行统计,制成如下频率分布表:
序号 | 分数段 | 人数 | 频率 |
1 |
| 10 | 0.20 |
2 |
| ① | 0.44 |
3 |
| ② | ③ |
4 |
| 4 | 0.08 |
合计 | 50 | 1 | |
(1)填充上述表中的空格(在解答中直接写出对应空格序号的答案);
(2)若利用组中值近似计算数据的平均数,求此次数学史初赛的平均成绩;
(3)甲同学的初赛成绩在![]() ,学校为了宣传班级的学习经验,随机抽取分数在
,学校为了宣传班级的学习经验,随机抽取分数在![]() 的4位同学中的两位同学到学校其他班级介绍,求甲同学被抽取到的概率.
的4位同学中的两位同学到学校其他班级介绍,求甲同学被抽取到的概率.