题目内容
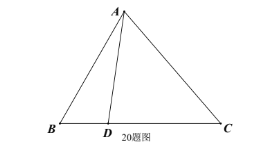
【题目】在△ABC中，D为BC上一点，AD=CD，BA=7，BC=8。
(1)若B=60°，求△ABC外接圆的半径R；
(2)设
，若
，求△ABC面积。
【答案】（1）
；（2）
【解析】
（1）在△ABC中由余弦定理得
，然后再根据正弦定理可求得外接圆的半径．（2）由条件可得
，故得
，设BD=
，则DC=8
，DA=8，在△ABD中由余弦定理得
，进而
，再由正弦定理得
，于是可求得三角形的面积．
(1) 在△ABC中，由余弦定理得
，
所以，
由正弦定理得
，
所以
．
故△ABC外接圆的半径R为．
(2)由AD=CD，得∠DCA=∠DAC，
所以
．
由
，
得．
设BD=，则DC=8，DA=8.
在△ABD中，
，
由余弦定理得
，
得．
所以BD=3，DA=5，
由正弦定理得
，即
，
所以．
所以
．
故
．
练习册系列答案
相关题目
【题目】下面有两个关于“袋子中装有红、白两种颜色的相同小球，从袋中无放回地取球”的游戏规则，这两个游戏规则公平吗？为什么？
游 戏 1 | 游 戏 2 |
2个红球和2个白球 | 3个红球和1个白球 |
取1个球，再取1个球 | 取1个球，再取1个球 |
取出的两个球同色→甲胜 | 取出的两个球同色→甲胜 |
取出的两个球不同色→乙胜 | 取出的两个球不同色→乙胜 |
