题目内容
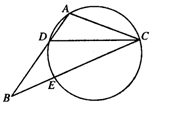
如图,在△ABC中,CD是∠ACB的角平分线,△ADC的外接圆交BC于点E,AB=2AC
(1)求证:BE=2AD;
(2)当AC=3,EC=6时,求AD的长.
(1)求证:BE=2AD;
(2)当AC=3,EC=6时,求AD的长.

(1)详见解析 (2)

试题分析:(1)连接
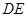 ,因为
,因为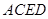 是圆的内接四边形,所以
是圆的内接四边形,所以 ,能够得到线段的比例关系,由此能够证明
,能够得到线段的比例关系,由此能够证明
(2)由条件得
 ,设
,设 ,根据割线定理得
,根据割线定理得 ,即
,即 ,由此能求出
,由此能求出 .
.(1)连接
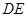 ,因为
,因为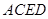 是圆内接四边形,所以
是圆内接四边形,所以
又

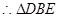 ∽
∽ ,即有
,即有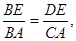
又因为
 ,可得
,可得
因为
 是
是 的平分线,所以
的平分线,所以 ,
,从而
 ; 5分
; 5分
(2)由条件知
 ,设
,设 ,
,则
 ,根据割线定理得
,根据割线定理得 ,
,即
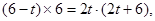 即
即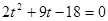 ,
,解得
 或
或 (舍去),则
(舍去),则 10分
10分
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 AD,从AB的中点F作HF⊥EC于H.
AD,从AB的中点F作HF⊥EC于H.



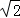 ,AF:FB:BE=4:2:1.若CE与圆相切,则CE的长为 .
,AF:FB:BE=4:2:1.若CE与圆相切,则CE的长为 .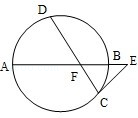
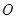 的两条弦, AB与CD相交于点E,且
的两条弦, AB与CD相交于点E,且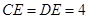 ,
,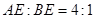 ,则
,则 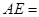 ______;
______;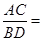 ______.
______.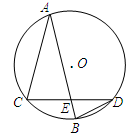

 ,OA=
,OA=