题目内容

10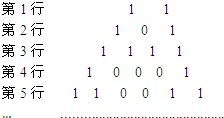．将杨辉三角中的奇数换成1，偶数换成0，得到如图所示的0-1三角数表、从上往下数，第1次全行的数都为1的是第1行，第2次全行的数都为1的是第3行，…，第n次全行的数都为1的是第2n-1行；第62行中1的个数是32．

分析 本题考查的知识点是归纳推理，我们可以根据图中三角形是将杨辉三角中的奇数换成1，偶数换成0，结合杨辉三角我们易得到第1行，第3行，第7行，…全都是1，则归纳推断可得：第n次全行的数都为1的是第2n-1行；由此结论我们可得第63行共有64个1，逆推即可得到第62行中1的个数

解答 解：由已知中的数据
第1行          1   1
第2行        1   0   1
第3行       1   1  1   1
第4行      1   0  0  0   1
第5行     1  1   0  0   1   1
…
全行都为1的是第2n-1行；
全行都为1的是第2n-1行；
∵n=6⇒26-1=63，
故第63行共有64个1，
逆推知第62行共有32个1，
故答案为：32．

点评 本题考查了归纳推理，归纳推理的一般步骤是：（1）通过观察个别情况发现某些相同性质，（2）从已知某些相同性质中推出一个明确表达的一般性命题

练习册系列答案
相关题目
20．关于△ABC有如下命题：在正三角形ABC内部（不包括边界）任取一点P，P点到三边的距离分别为h1，h2，h3，则h1+h2+h3为定值，证明如下：连接PB、PC、PA，设△PBC、△PCA、△PAB的面积分别为S1，S2，S3，△ABC的面积为S，则有：S=S1+S2+S3⇒h=h1+h2+h3（其中h为△ABC的高），根据上述思维猜想在正四面体（四个面均为正三角形的三棱锥）中的结论，并对猜想进行证明．
1．已知平面上四点O、A、B、C满足∠AOB=120°，∠BOC=90°，|$\overrightarrow{OA}$|=2，|$\overrightarrow{OB}$|=1，$\overrightarrow{OA}$=x$\overrightarrow{OB}$+y$\overrightarrow{OC}$，若x+y=-4，则|$\overrightarrow{OC}$|=$\frac{\sqrt{3}}{3}$．
18．已知偶函数f（x）=ax2+bx+c（a，b，c∈R）在点（1，1）处的切线与直线x+2y+9=0垂直，函数g（x）=f（x）+mln（x+1）（m≠0）．
（Ⅰ）求函数f（x）的解析式．
（Ⅱ）当m＜$\frac{1}{2}$时，求函数g（x）的单调区间和极值点；
（Ⅲ）证明：对于任意实数x，不等式ln（ex+1）＞e2x-e3x恒成立．（其中e=2.71828…是自然对数的底数）
5．已知随机变量x服从二项分布x～B（6，$\frac{1}{3}$），则P（x=2）等于（　　）
A．$\frac{80}{243}$B．$\frac{4}{243}$C．$\frac{13}{243}$D．$\frac{13}{16}$
15．若（2x+$\sqrt{3}$）100=a0+a1x+a2x2+…+a100x100，则（a0+a2+a4+…+a100）2-（a1+a3+a5+…+a99）2的值为（　　）
A．1B．-1C．0D．2
2．当输入x=-1，y=20时，如图中程序运行后输出的结果为  （　　）
A．3； 43B．43；3C．-18；16D．16；-18
19．否定“自然数m，n，k中恰有一个奇数”时正确的反设为（　　）
A．m，n，k都是奇数B．m，n，k都是偶数
C．m，n，k中至少有两个偶数D．m，n，k都是偶数或至少有两个奇数
20．在边长为2的菱形ABCD中，∠BAD=60°，M，N分别为边BC，CD的中点．

（1）用$\overrightarrow{AB}$、$\overrightarrow{AD}$表示$\overrightarrow{MN}$；
（2）求$\overrightarrow{AM}•\overrightarrow{AN}$的值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网