题目内容
19．否定“自然数m，n，k中恰有一个奇数”时正确的反设为（ ）| A． | m，n，k都是奇数 | B． | m，n，k都是偶数 | ||
| C． | m，n，k中至少有两个偶数 | D． | m，n，k都是偶数或至少有两个奇数 |
分析 求得命题：“自然数m，n，k中恰有一个奇数”的否定，即可得出结论．
解答 解：由于命题：“自然数m，n，k中恰有一个奇数”的否定为：“m，n，k都是偶数或至少有两个奇数”，
故否定“自然数m，n，k中恰有一个奇数”时正确的反设为：“m，n，k都是偶数或至少有两个奇数”，
故选：D．
点评 本题主要考查反证法，求一个命题的否定，属于基础题．
练习册系列答案
学练快车道口算心算速算天天练系列答案
相关题目
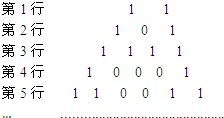将杨辉三角中的奇数换成1，偶数换成0，得到如图所示的0-1三角数表、从上往下数，第1次全行的数都为1的是第1行，第2次全行的数都为1的是第3行，…，第n次全行的数都为1的是第2n-1行；第62行中1的个数是32．
7．已知$tan（α+\frac{π}{5}）=2$，$tan（β-\frac{4π}{5}）=-3$，则tan（α-β）=（ ）
| A． | 1 | B． | -$\frac{5}{7}$ | C． | $\frac{5}{7}$ | D． | -1 |
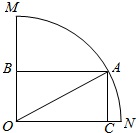如图：已知扇形MON所在圆半径为1，∠MON=$\frac{π}{2}$，扇形内接矩形ABOC，设∠AON=θ．
11．已知数列{an}的通项公式是an=$\frac{n+2}{n+1}$，则这个数列是（ ）
| A． | 递增数列 | B． | 递减数列 | C． | 常数列 | D． | 摆动数列 |
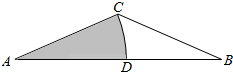如图，在一个等腰三角形ABC内以A为圆心，腰AC长为半径画弧交底边AB于D，已知AC=1，∠A=30°，现向△ABC内任投一点，该点落在图中阴影部分的概率为$\frac{\sqrt{3}π}{9}$．