题目内容
20.在边长为2的菱形ABCD中,∠BAD=60°,M,N分别为边BC,CD的中点.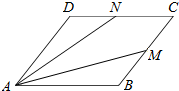
(1)用$\overrightarrow{AB}$、$\overrightarrow{AD}$表示$\overrightarrow{MN}$;
(2)求$\overrightarrow{AM}•\overrightarrow{AN}$的值.
分析 (1)在△AMN中,$\overrightarrow{MN}=\overrightarrow{AN}-\overrightarrow{AM}=\overrightarrow{AD}+\overrightarrow{DN}-({\overrightarrow{AB}+\overrightarrow{BM}})$,利用中点性质得到所求;
(2)首先将$\overrightarrow{AM},\overrightarrow{AN}$分别用向量$\overrightarrow{AB}$,$\overrightarrow{AD}$表示,然后进行数量积的运算.
解答 解:(1)由题,在△AMN中,$\overrightarrow{MN}=\overrightarrow{AN}-\overrightarrow{AM}=\overrightarrow{AD}+\overrightarrow{DN}-({\overrightarrow{AB}+\overrightarrow{BM}})$=$\overrightarrow{AD}+\frac{1}{2}\overrightarrow{AB}-({\overrightarrow{AB}+\frac{1}{2}\overrightarrow{AD}})=\frac{1}{2}\overrightarrow{AD}-\frac{1}{2}\overrightarrow{AB}$…(7分)
(2)在△ABM,$\overrightarrow{AM}=\overrightarrow{AB}+\overrightarrow{BM}=\overrightarrow{AB}+\frac{1}{2}\overrightarrow{BC}=\overrightarrow{AB}+\frac{1}{2}\overrightarrow{AD}$…(9分)
同理,在△ADN,$\overrightarrow{AN}=\overrightarrow{AD}+\frac{1}{2}\overrightarrow{AB}$…(11分)
所以$\overrightarrow{AM}•\overrightarrow{AN}=({\overrightarrow{AB}+\frac{1}{2}\overrightarrow{AD}})({\overrightarrow{AD}+\frac{1}{2}\overrightarrow{AB}})$=$\frac{1}{2}{\overrightarrow{AB}^2}+\frac{1}{2}{\overrightarrow{AD}^2}+\frac{5}{4}\overrightarrow{AB}•\overrightarrow{AD}=\frac{1}{2}×4+\frac{1}{2}×4+\frac{5}{4}×2×2×\frac{1}{2}=\frac{13}{2}$…(14分)
点评 本题考查了向量的三角形法则的运用以及向量数量积的运算;属于基础题.

 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案| A. | 递增数列 | B. | 递减数列 | C. | 常数列 | D. | 摆动数列 |
| A. | (1,+∞) | B. | (e,+∞) | C. | (0,1) | D. | (0,e) |
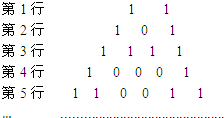 将杨辉三角中的奇数换成1,偶数换成0,得到如图所示的0-1三角数表、从上往下数,第1次全行的数都为1的是第1行,第2次全行的数都为1的是第3行,…,第n次全行的数都为1的是第2n-1行;第62行中1的个数是32.
将杨辉三角中的奇数换成1,偶数换成0,得到如图所示的0-1三角数表、从上往下数,第1次全行的数都为1的是第1行,第2次全行的数都为1的是第3行,…,第n次全行的数都为1的是第2n-1行;第62行中1的个数是32. 如图,在一个等腰三角形ABC内以A为圆心,腰AC长为半径画弧交底边AB于D,已知AC=1,∠A=30°,现向△ABC内任投一点,该点落在图中阴影部分的概率为$\frac{\sqrt{3}π}{9}$.
如图,在一个等腰三角形ABC内以A为圆心,腰AC长为半径画弧交底边AB于D,已知AC=1,∠A=30°,现向△ABC内任投一点,该点落在图中阴影部分的概率为$\frac{\sqrt{3}π}{9}$.