题目内容
5．已知随机变量x服从二项分布x～B（6，$\frac{1}{3}$），则P（x=2）等于（ ）| A． | $\frac{80}{243}$ | B． | $\frac{4}{243}$ | C． | $\frac{13}{243}$ | D． | $\frac{13}{16}$ |
分析 随机变量x服从二项分布x～B（6，$\frac{1}{3}$），表示6次独立重复试验，每次实验成功概率为$\frac{1}{3}$，P（x=2）表示6次试验中成功两次的概率．
解答 解：随机变量x服从二项分布x～B（6，$\frac{1}{3}$），
则P（x=2）=${C}_{6}^{2}（{\frac{1}{3}）}^{2}（\frac{2}{3}）^{4}$=$\frac{80}{243}$
故选：A．
点评 本题考查独立重复试验中事件的概率及二项分布知识，属基本题．
练习册系列答案
步步高达标卷系列答案
相关题目
15．已知集合A={（x，y）|x+2y-4=0}，集合B={（x，y）|x=0}，则A∩B=（ ）
| A． | {0，2} | B． | {（0，2）} | C． | （0，2） | D． | ∅ |
16．双曲线方程：$\frac{{x}^{2}}{|k|-2}$+$\frac{{y}^{2}}{5-k}$=1，那么k的取值范围是（ ）
| A． | （5，+∞） | B． | （2，5） | C． | （-2，2） | D． | （-2，2）或（5，+∞） |
13．设随机变量X的概率分布列为
则P（|X-3|=1）=（ ）
| X | 1 | 2 | 3 | 4 |
| P | $\frac{1}{3}$ | m | $\frac{1}{4}$ | $\frac{1}{6}$ |
| A． | $\frac{7}{12}$ | B． | $\frac{5}{12}$ | C． | $\frac{1}{4}$ | D． | $\frac{1}{6}$ |
20．若函数f（x）=sinx+ax在R上单调递增，则实数a的取值范围为（ ）
| A． | [-1，1] | B． | （-∞，-1] | C． | （-∞，1] | D． | [1，+∞） |
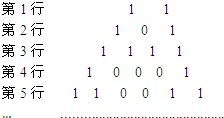将杨辉三角中的奇数换成1，偶数换成0，得到如图所示的0-1三角数表、从上往下数，第1次全行的数都为1的是第1行，第2次全行的数都为1的是第3行，…，第n次全行的数都为1的是第2n-1行；第62行中1的个数是32．
17．若下表数据对应的y关于x的线性回归方程为$\hat y=0.7x+a$，则a=0.35．
| x | 3 | 4 | 5 | 6 |
| y | 2.5 | 3 | 4 | 4.5 |
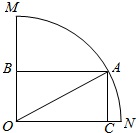如图：已知扇形MON所在圆半径为1，∠MON=$\frac{π}{2}$，扇形内接矩形ABOC，设∠AON=θ．