题目内容
1.已知平面上四点O、A、B、C满足∠AOB=120°,∠BOC=90°,|$\overrightarrow{OA}$|=2,|$\overrightarrow{OB}$|=1,$\overrightarrow{OA}$=x$\overrightarrow{OB}$+y$\overrightarrow{OC}$,若x+y=-4,则|$\overrightarrow{OC}$|=$\frac{\sqrt{3}}{3}$.分析 如图所示,A$(-1,\sqrt{3})$,B(1,0),设C(0,c).利用$\overrightarrow{OA}$=x$\overrightarrow{OB}$+y$\overrightarrow{OC}$,及其向量坐标运算即可得出.
解答 解:如图所示,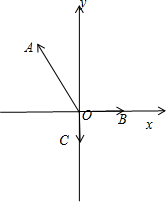
A$(-1,\sqrt{3})$,B(1,0),设C(0,c).
∵$\overrightarrow{OA}$=x$\overrightarrow{OB}$+y$\overrightarrow{OC}$,
∴$(-1,\sqrt{3})$=x(1,0)+y(0,c).
∴$\left\{\begin{array}{l}{-1=x}\\{\sqrt{3}=yc}\end{array}\right.$,又x+y=-4.
∴x=-1,y=-3,
c=-$\frac{\sqrt{3}}{3}$.
∴$|\overrightarrow{OC}|$=$\frac{\sqrt{3}}{3}$.
故答案为:$\frac{\sqrt{3}}{3}$.
点评 本题考查了向量的坐标运算、共线定理、模的计算公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案
相关题目
16.双曲线方程:$\frac{{x}^{2}}{|k|-2}$+$\frac{{y}^{2}}{5-k}$=1,那么k的取值范围是( )
| A. | (5,+∞) | B. | (2,5) | C. | (-2,2) | D. | (-2,2)或(5,+∞) |
6.在正四面体ABCD中,点E,F分别是AB,BC的中点,则下列结论错误的是( )
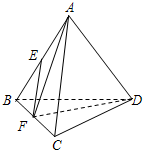

| A. | 异面直线AB与CD所成的角为90° | B. | 直线AB与平面BCD成的角为60° | ||
| C. | 直线EF∥平面ACD | D. | 平面AFD垂直平面BCD |
13.设随机变量X的概率分布列为
则P(|X-3|=1)=( )
| X | 1 | 2 | 3 | 4 |
| P | $\frac{1}{3}$ | m | $\frac{1}{4}$ | $\frac{1}{6}$ |
| A. | $\frac{7}{12}$ | B. | $\frac{5}{12}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{6}$ |
11.已知数列{an}的通项公式是an=$\frac{n+2}{n+1}$,则这个数列是( )
| A. | 递增数列 | B. | 递减数列 | C. | 常数列 | D. | 摆动数列 |
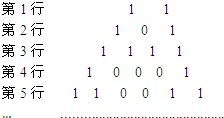 将杨辉三角中的奇数换成1,偶数换成0,得到如图所示的0-1三角数表、从上往下数,第1次全行的数都为1的是第1行,第2次全行的数都为1的是第3行,…,第n次全行的数都为1的是第2n-1行;第62行中1的个数是32.
将杨辉三角中的奇数换成1,偶数换成0,得到如图所示的0-1三角数表、从上往下数,第1次全行的数都为1的是第1行,第2次全行的数都为1的是第3行,…,第n次全行的数都为1的是第2n-1行;第62行中1的个数是32.