题目内容
18.已知偶函数f(x)=ax2+bx+c(a,b,c∈R)在点(1,1)处的切线与直线x+2y+9=0垂直,函数g(x)=f(x)+mln(x+1)(m≠0).(Ⅰ)求函数f(x)的解析式.
(Ⅱ)当m<$\frac{1}{2}$时,求函数g(x)的单调区间和极值点;
(Ⅲ)证明:对于任意实数x,不等式ln(ex+1)>e2x-e3x恒成立.(其中e=2.71828…是自然对数的底数)
分析 (Ⅰ)根据函数为偶函数,得到b=0,再根据导数的几何意义求,解得a,c,继而得到函数的解析式;
(Ⅱ)先求导,注意定义域,令g'(x)=0,解得x1,x2,根据导数和函数的单调性的关系求出极值和单调区间;
(Ⅲ)构造函数h(x)=x3-x2+ln(x+1),利用导数求出函数的最值,问题得以证明.
解答 (Ⅰ)因为f(x)为偶函数,所以b=0.
因为f'(x)=2ax+b=2ax,由题意知$\left\{\begin{array}{l}a+c=1\\ 2a•(-\frac{1}{2})=-1\end{array}\right.$解得$\left\{\begin{array}{l}a=1\\ c=0\end{array}\right.$
所以f(x)=x2.
(Ⅱ)g(x)=x2+mln(x+1)由题意知,g(x)的定义域为(-1,+∞),$g'(x)=2x+\frac{m}{x+1}=\frac{{2{x^2}+2x+m}}{x+1}$.
因为$m<\frac{1}{2}$,则g'(x)=0有两个不同解,${x_1}=\frac{{-1-\sqrt{1-2m}}}{2},{x_2}=\frac{{-1+\sqrt{1-2m}}}{2}$.
①若m<0,${x_1}=\frac{{-1-\sqrt{1-2m}}}{2}<-1,{x_2}=\frac{{-1+\sqrt{1-2m}}}{2}>-1$,
即x1∉(-1,+∞),x2∈(-1,+∞).
此时,当x变化时,g'(x),g(x)随x的变化情况如下表:
| x | (-1,x2) | x2 | (x2,+∞) |
| g'(x) | - | 0 | + |
| g(x) | ↘ | 极小值 | ↗ |
②若$0<m<\frac{1}{2}$,${x_1}=\frac{{-1-\sqrt{1-2m}}}{2}>-1$,∴x1,x2∈(-1,+∞),
此时,当x变化时,g'(x),g(x)随x的变化情况如下表:
| x | (-1,x1) | x1 | (x1,x2) | x2 | (x2,+∞) |
| g'(x) | + | 0 | - | 0 | + |
| g(x) | ↗ | 极大值 | ↘ | 极小值 | ↗ |
单调递减区间为$(\frac{{-1-\sqrt{1-2m}}}{2},\frac{{-1+\sqrt{1-2m}}}{2})$;
函数g(x)有一个极大值点$x=\frac{{-1-\sqrt{1-2m}}}{2}$和一个极小值点$x=\frac{{-1+\sqrt{1-2m}}}{2}$.
综上所述:①若m<0,函数g(x)的单调递增区间为$(\frac{{-1+\sqrt{1-2m}}}{2},+∞)$,单调递减区间为$(-1,\frac{{-1+\sqrt{1-2m}}}{2})$;
g(x)有唯一极小值点$x=\frac{{-1+\sqrt{1-2m}}}{2}$;
②若$0<m<\frac{1}{2}$,函数g(x)的单调递增区间为$(-1,\frac{{-1-\sqrt{1-2m}}}{2})$,$(\frac{{-1+\sqrt{1-2m}}}{2},+∞)$,单调递减区间为$(\frac{{-1-\sqrt{1-2m}}}{2},\frac{{-1+\sqrt{1-2m}}}{2})$;
函数g(x)有一个极大值点$x=\frac{{-1-\sqrt{1-2m}}}{2}$和一个极小值点$x=\frac{{-1+\sqrt{1-2m}}}{2}$.
(Ⅲ) 当m=-1时,函数g(x)=x2-ln(x+1),令函数h(x)=x3-g(x)=x3-x2+ln(x+1)
则$h'(x)=3{x^2}-2x+\frac{1}{x+1}=\frac{{3{x^3}+{{(x-1)}^2}}}{x+1}$,
所以当x∈(0,+∞)时,h'(x)>0,所以函数h(x)在(0,+∞)上单调递增,
又h(0)=0,则x∈(0,+∞)时,恒有h(x)>h(0),即x3>x2-ln(x+1)恒成立.
故当x∈(0,+∞)时,有ln(x+1)>x2-x3.
所以?x∈R,不等式ln(ex+1)>e2x-e3x恒成立.
点评 本题是利用导数研究函数的单调性、求函数的极值的基本题型,考查了分类讨论的思想,关键是抓住分类的标准,属于难题.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目
6.在正四面体ABCD中,点E,F分别是AB,BC的中点,则下列结论错误的是( )
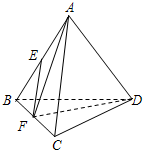

| A. | 异面直线AB与CD所成的角为90° | B. | 直线AB与平面BCD成的角为60° | ||
| C. | 直线EF∥平面ACD | D. | 平面AFD垂直平面BCD |
13.设随机变量X的概率分布列为
则P(|X-3|=1)=( )
| X | 1 | 2 | 3 | 4 |
| P | $\frac{1}{3}$ | m | $\frac{1}{4}$ | $\frac{1}{6}$ |
| A. | $\frac{7}{12}$ | B. | $\frac{5}{12}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{6}$ |
7.已知$tan(α+\frac{π}{5})=2$,$tan(β-\frac{4π}{5})=-3$,则tan(α-β)=( )
| A. | 1 | B. | -$\frac{5}{7}$ | C. | $\frac{5}{7}$ | D. | -1 |
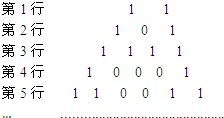 将杨辉三角中的奇数换成1,偶数换成0,得到如图所示的0-1三角数表、从上往下数,第1次全行的数都为1的是第1行,第2次全行的数都为1的是第3行,…,第n次全行的数都为1的是第2n-1行;第62行中1的个数是32.
将杨辉三角中的奇数换成1,偶数换成0,得到如图所示的0-1三角数表、从上往下数,第1次全行的数都为1的是第1行,第2次全行的数都为1的是第3行,…,第n次全行的数都为1的是第2n-1行;第62行中1的个数是32.