题目内容
11.定义在区间[a,b]上的函数f(x)=$\frac{1}{2}$sinx-$\frac{\sqrt{3}}{2}$cosx的值域是[-$\frac{1}{2}$,1],则b-a的最大值是$\frac{4π}{3}$.分析 由题意根据f(x)=sin(x-$\frac{π}{3}$)的值域是[-$\frac{1}{2}$,1],求得x-$\frac{π}{3}$的最大范围为[2kπ-$\frac{π}{6}$,2kπ+$\frac{7π}{6}$],k∈z,可得x的最大范围,从而求得b-a的最大值.
解答 解:定义在区间[a,b]上的函数f(x)=$\frac{1}{2}$sinx-$\frac{\sqrt{3}}{2}$cosx=sin(x-$\frac{π}{3}$)的值域是[-$\frac{1}{2}$,1],
则x-$\frac{π}{3}$的最大范围为[2kπ-$\frac{π}{6}$,2kπ+$\frac{7π}{6}$],k∈z,可得x的最大范围为[2kπ-$\frac{π}{2}$,2kπ+$\frac{5π}{6}$],k∈z,
故b-a的最大值为$\frac{5π}{6}$-(-$\frac{π}{2}$)=$\frac{4π}{3}$,
故答案为:$\frac{4π}{3}$.
点评 本题主要考查两角和差的正弦公式,正弦函数的定义域和值域,求得x-$\frac{π}{3}$的最大范围为[2kπ-$\frac{π}{6}$,2kπ+$\frac{7π}{6}$],k∈z,是解题的关键,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
20.若a,b,c∈(0,+∞),且a+b+c=1,则$\frac{1}{a+b}$+$\frac{1}{b+c}$+$\frac{1}{c+a}$的最小值为( )
| A. | $\frac{1}{3}$ | B. | $\frac{\root{3}{2}}{3}$ | C. | $\frac{9}{2}$ | D. | $\frac{1}{9}$ |
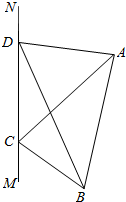 如图,为对某失事客轮AB进行有效援助,现分别在河岸MN选择两处C、D用强光柱进行辅助照明,其中A、B、C、D在同一平面内.现测得CD长为100米,∠ADN=105°,∠BDM=30°,∠ACN=45°,∠BCM=60°.
如图,为对某失事客轮AB进行有效援助,现分别在河岸MN选择两处C、D用强光柱进行辅助照明,其中A、B、C、D在同一平面内.现测得CD长为100米,∠ADN=105°,∠BDM=30°,∠ACN=45°,∠BCM=60°.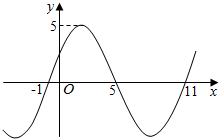 函数f(x)=Asin(ωx+φ)(A>0,ω>0)在R上的部分图象如图所示,则ω的值为$\frac{π}{6}$.
函数f(x)=Asin(ωx+φ)(A>0,ω>0)在R上的部分图象如图所示,则ω的值为$\frac{π}{6}$.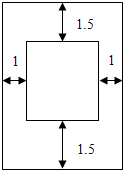 某出版社出版一读物,为了排版设计的需要,规定:一页上所印文字的矩形区域需要占去150cm2,上、下边各要留1.5cm宽的空白,左、右两边各要留1cm宽的空白,出版商为了节约纸张,应选用怎样尺寸的矩形纸张来设计版面?
某出版社出版一读物,为了排版设计的需要,规定:一页上所印文字的矩形区域需要占去150cm2,上、下边各要留1.5cm宽的空白,左、右两边各要留1cm宽的空白,出版商为了节约纸张,应选用怎样尺寸的矩形纸张来设计版面?