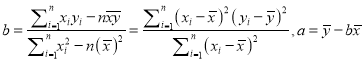题目内容
【题目】已知f(x)=aln(x2+1)+bx存在两个极值点x1 , x2 .
(1)求证:|x1+x2|>2;
(2)若实数λ满足等式f(x1)+f(x2)+a+λb=0,试求λ的取值范围.
【答案】
(1)证明:由f(x)=aln(x2+1)+bx的导数为f′(x)= ![]() +b=
+b= ![]() ,
,
令g(x)=bx2+2ax+b,由题意可得g(x)=0有两个不同的非零实根,
得△=4a2﹣4b2>0,
因此a>b>0,
所以 ![]() >1;
>1;
所以x1+x2=﹣ ![]() <﹣2,
<﹣2,
即|x1+x2|>2
(2)解:由(1)知x1x2=1,
f(x1)+f(x2)+a
=aln[x12x22+(x12+x22)+1]+b(x1+x2)+a
=aln[(x12+x22)+2]+b(x1+x2)+a
=aln[(x1+x2)2]+b(x1+x2)+a
=2aln ![]() ﹣a,
﹣a,
由f(x1)+f(x2)+a+λb=0得﹣λ= ![]() ln
ln ![]() ﹣
﹣ ![]() ,
,
设t= ![]() >2,则﹣λ=tlnt﹣
>2,则﹣λ=tlnt﹣ ![]() t,
t,
令h(t)=tlnt﹣ ![]() t,t>2.
t,t>2.
h′(t)=1+lnt﹣ ![]() =lnt+
=lnt+ ![]() >0,
>0,
h(t)在(2,+∞)是增函数.
因此﹣λ>2ln2﹣1,
即为λ<1﹣2ln2
【解析】(1)由f(x)的导数,可设g(x)=f′(x),即有方程g(x)=0有两个不同的非零实根x1 , x2 , 可得 ![]() >1,结合韦达定理可得结论;(2)若实数λ满足等式f(x1)+f(x2)+a+λb=0,化简整理可得﹣λ=
>1,结合韦达定理可得结论;(2)若实数λ满足等式f(x1)+f(x2)+a+λb=0,化简整理可得﹣λ= ![]() ln
ln ![]() ﹣
﹣ ![]() ,设t=
,设t= ![]() >2,则﹣λ=tlnt﹣
>2,则﹣λ=tlnt﹣ ![]() t,求出右边函数的导数,判断单调性,进而可得λ的取值范围.
t,求出右边函数的导数,判断单调性,进而可得λ的取值范围.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案
相关题目