题目内容
如图,底面是矩形的四棱锥P—ABCD中AB=2,BC= ,侧面PAB是等边三角形,且侧面PAB⊥底面ABCD.
,侧面PAB是等边三角形,且侧面PAB⊥底面ABCD.
(1)证明:侧面PAB⊥侧面PBC;
(2)求侧棱PC与底面ABCD所成的角;(3)求直线AB与平面PCD的距离.
 ,侧面PAB是等边三角形,且侧面PAB⊥底面ABCD.
,侧面PAB是等边三角形,且侧面PAB⊥底面ABCD. (1)证明:侧面PAB⊥侧面PBC;
|

(1)见解析
(2)45°
(3)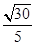
(2)45°
(3)
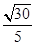
本试题主要是考查了立体几何中,面面垂直问题,以及线面角的求解,和线面的距离的相关知识的理解和运用。侧重在判定定理和性质定理的灵活运用上。
(I)证明:在矩形ABCD中,BC⊥AB 又∵面PAB⊥底面ABCD侧面PAB∩底面ABCD=AB ∴BC⊥侧面PAB 又∵BC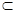 侧面PBC ∴侧面PAB⊥侧面PBC) 4分
侧面PBC ∴侧面PAB⊥侧面PBC) 4分
(II)解:取AB中点E,连结PE、CE 又∵△PAB是等边三角形 ∴PE⊥AB
又∵侧面PAB⊥底面ABCD,∴PE⊥面ABCD ∴∠PCE为侧棱PC与底面ABCD所成角
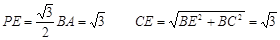 在Rt△PEC中,∠PCE=45°为所求
在Rt△PEC中,∠PCE=45°为所求
(Ⅲ)解:在矩形ABCD中,AB//CD ∵CD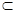 侧面PCD,AB
侧面PCD,AB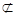 侧面PCD,∴AB//侧面PCD
侧面PCD,∴AB//侧面PCD
取CD中点F,连EF、PF,则EF⊥AB 又∵PE⊥AB ∴AB⊥平面PEF 又∵AB//CD
∴CD⊥平面PEF ∴平面PCD⊥平面PEF 作EG⊥PF,垂足为G,则EC⊥平面PCD
在Rt△PEF中,EG=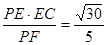 为所求.
为所求.
(I)证明:在矩形ABCD中,BC⊥AB 又∵面PAB⊥底面ABCD侧面PAB∩底面ABCD=AB ∴BC⊥侧面PAB 又∵BC
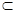 侧面PBC ∴侧面PAB⊥侧面PBC) 4分
侧面PBC ∴侧面PAB⊥侧面PBC) 4分(II)解:取AB中点E,连结PE、CE 又∵△PAB是等边三角形 ∴PE⊥AB
又∵侧面PAB⊥底面ABCD,∴PE⊥面ABCD ∴∠PCE为侧棱PC与底面ABCD所成角
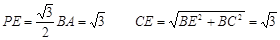 在Rt△PEC中,∠PCE=45°为所求
在Rt△PEC中,∠PCE=45°为所求(Ⅲ)解:在矩形ABCD中,AB//CD ∵CD
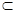 侧面PCD,AB
侧面PCD,AB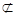 侧面PCD,∴AB//侧面PCD
侧面PCD,∴AB//侧面PCD取CD中点F,连EF、PF,则EF⊥AB 又∵PE⊥AB ∴AB⊥平面PEF 又∵AB//CD
∴CD⊥平面PEF ∴平面PCD⊥平面PEF 作EG⊥PF,垂足为G,则EC⊥平面PCD
在Rt△PEF中,EG=
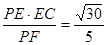 为所求.
为所求.
练习册系列答案
相关题目
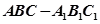 中,
中,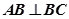 ,
,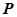 为
为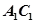 的中点,且
的中点,且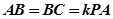 ,
,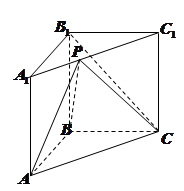
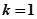 时,求证:
时,求证: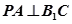 ;
;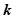 为何值时,直线
为何值时,直线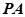 与平面
与平面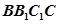 所成的角的正弦值为
所成的角的正弦值为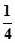 ,并求此时二面角
,并求此时二面角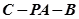 的余弦值。
的余弦值。 中,
中, 是
是 的中点,
的中点, 是线段
是线段 上一点,且
上一点,且 .
. ;
; 平面
平面 ,求
,求 的值.[
的值.[
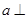 直线
直线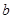 ,a,b异面,
,a,b异面,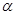 ,
,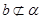 。求证:
。求证: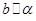 。
。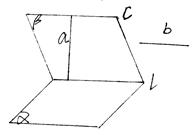
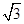 ,AA1=
,AA1=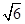 ,M为侧棱CC1上一点,AM⊥BA1。
,M为侧棱CC1上一点,AM⊥BA1。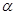 //平面β,点
//平面β,点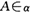 ,直线
,直线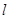 经过点A,则“
经过点A,则“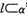 ”是“
”是“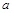 ,
,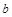 ,
,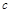 中,若
中,若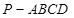 中,底面
中,底面 为菱形,
为菱形,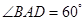 ,
,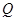 为
为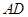 的中点,
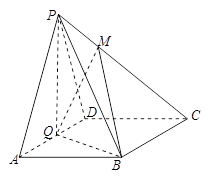
的中点,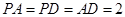 .
.
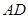
 平面
平面 ;
;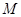 在线段
在线段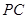 上,
上,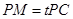 ,试确定
,试确定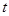 的值,使
的值,使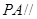 平面
平面 ;
;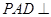 平面
平面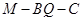 的大小.
的大小. 中,四边形
中,四边形 为平行四边形,且面
为平行四边形,且面 面
面 ,
,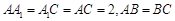 ,且
,且 ,
, 为
为 中点.
中点. 平面
平面 与平面
与平面 所成角的正弦值.
所成角的正弦值.