题目内容
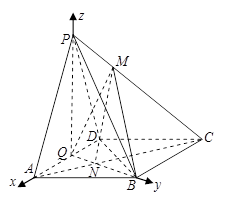
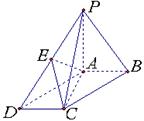
(本小题共14分)如图,在四棱锥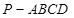 中,底面
中,底面 为菱形,
为菱形,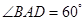 ,
,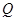 为
为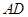 的中点,
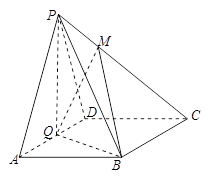
的中点,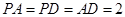 .
.
(Ⅰ)求证: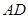
 平面
平面 ;
;
(Ⅱ)点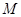 在线段
在线段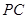 上,
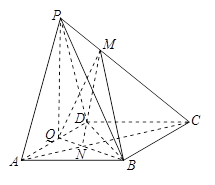
上,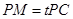 ,试确定
,试确定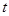 的值,使
的值,使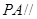 平面
平面 ;
;
(Ⅲ)若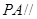 平面
平面 ,平面
,平面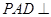 平面
平面 ,求二面角
,求二面角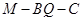 的大小.
的大小.
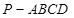 中,底面
中,底面 为菱形,
为菱形,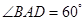 ,
,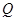 为
为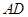 的中点,
的中点,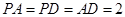 .
.
(Ⅰ)求证:
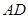
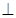 平面
平面 ;
;(Ⅱ)点
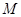 在线段
在线段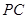 上,
上,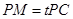 ,试确定
,试确定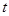 的值,使
的值,使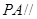 平面
平面 ;
;(Ⅲ)若
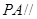 平面
平面 ,平面
,平面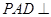 平面
平面 ,求二面角
,求二面角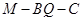 的大小.
的大小.证明:(Ⅰ)连接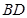 .
.
因为四边形 为菱形,
为菱形,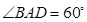 ,
,
所以△ 为正三角形.又
为正三角形.又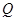 为
为 中点,
中点,
所以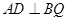 .
.
因为 ,
,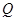 为
为 的中点,
的中点,
所以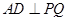 .
.
又 ,
,
所以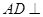 平面
平面 . ………………4分
. ………………4分
(Ⅱ)当 时,
时, ∥平面
∥平面 .
.
下面证明:
连接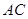 交
交 于
于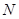 ,连接
,连接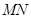 .
.
因为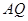 ∥
∥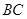 ,
,
所以 .
.
因为 ∥平面
∥平面 ,
,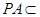 平面
平面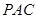 ,平面
,平面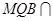 平面
平面
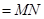 ,
,
所以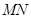 ∥
∥ .
.
所以 .
.
所以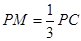 ,即
,即 .
.
因为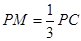 ,
,
所以 .
.
所以 ,
,
所以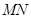 ∥
∥ .
.
又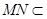 平面
平面 ,
,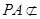 平面
平面 ,
,
所以 ∥平面
∥平面 . …………9分
. …………9分
(Ⅲ)因为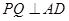 ,
,
又平面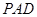
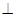 平面
平面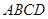 ,交线为
,交线为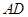 ,
,
所以 平面
平面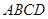 .
.
以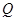 为坐标原点,分别以
为坐标原点,分别以 所在的直线为
所在的直线为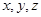 轴,建立如图所示的空间直
轴,建立如图所示的空间直
角坐标系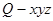 .
.
由 =
=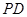 =
= =2,
=2,
则有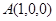 ,
,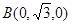 ,
,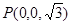 .
.
设平面 的法向量为
的法向量为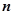 =
=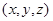 ,
,
由 ,
,
且 ,
,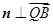 ,
,
可得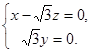
令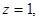 得
得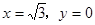 .
.
所以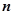 =
=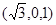 为平面
为平面 的一个法向量.
的一个法向量.
取平面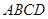 的法向量
的法向量 =
= ,
,
则
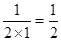 ,
,
故二面角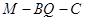 的大小为60°. …………14分
的大小为60°. …………14分
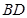 .
.因为四边形
 为菱形,
为菱形,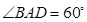 ,
,所以△
 为正三角形.又
为正三角形.又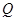 为
为 中点,
中点, 所以
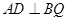 .
.因为
 ,
,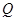 为
为 的中点,
的中点,所以
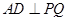 .
.又
 ,
, 所以
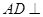 平面
平面 . ………………4分
. ………………4分(Ⅱ)当
 时,
时, ∥平面
∥平面 .
.下面证明:
连接
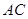 交
交 于
于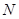 ,连接
,连接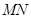 .
.
因为
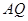 ∥
∥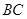 ,
,所以
 .
.因为
 ∥平面
∥平面 ,
,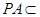 平面
平面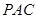 ,平面
,平面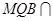 平面
平面
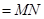 ,
,所以
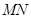 ∥
∥ .
.所以
 .
.所以
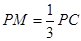 ,即
,即 .
.因为
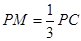 ,
,所以
 .
.所以
 ,
,所以
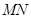 ∥
∥ .
.又
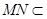 平面
平面 ,
,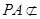 平面
平面 ,
,所以
 ∥平面
∥平面 . …………9分
. …………9分(Ⅲ)因为
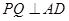 ,
,又平面
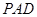
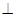 平面
平面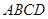 ,交线为
,交线为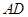 ,
,所以
 平面
平面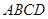 .
.以
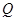 为坐标原点,分别以
为坐标原点,分别以 所在的直线为
所在的直线为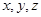 轴,建立如图所示的空间直
轴,建立如图所示的空间直角坐标系
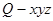 .
.
由
 =
=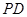 =
= =2,
=2,则有
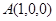 ,
,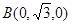 ,
,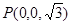 .
.设平面
 的法向量为
的法向量为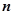 =
=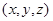 ,
,由
 ,
,
且
 ,
,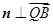 ,
,可得
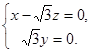
令
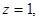 得
得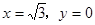 .
.所以
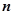 =
=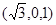 为平面
为平面 的一个法向量.
的一个法向量.取平面
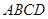 的法向量
的法向量 =
= ,
,则

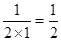 ,
,故二面角
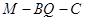 的大小为60°. …………14分
的大小为60°. …………14分本题考查线面垂直和二面角、探索性问题等综合问题。考查学生的空间想象能力。线面垂直的证明方法:(1)线面垂直的定义;(2)线面垂直的判断定理;(3)面面垂直的性质定理;(4)向量法:证明这个直线的方向向量和这个平面的法向量相互平行.
线面垂直的证明思考途径:线线垂直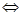 线面垂直
线面垂直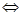 面面垂直.本题第一问利用方法二进行证明;探求某些点的具体位置,使得线面满足垂直关系,是一类逆向思维的题目.一般可采用两个方法:一是先假设存在,再去推理,下结论;二是运用推理证明计算得出结论,或先利用条件特例得出结论,然后再根据条件给出证明或计算.本题第二问主要采用假设存在点,然后确定线面平行的性质进行求解. 本题第三问利用向量法求解二面角.
面面垂直.本题第一问利用方法二进行证明;探求某些点的具体位置,使得线面满足垂直关系,是一类逆向思维的题目.一般可采用两个方法:一是先假设存在,再去推理,下结论;二是运用推理证明计算得出结论,或先利用条件特例得出结论,然后再根据条件给出证明或计算.本题第二问主要采用假设存在点,然后确定线面平行的性质进行求解. 本题第三问利用向量法求解二面角.
线面垂直的证明思考途径:线线垂直
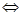 线面垂直
线面垂直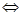 面面垂直.本题第一问利用方法二进行证明;探求某些点的具体位置,使得线面满足垂直关系,是一类逆向思维的题目.一般可采用两个方法:一是先假设存在,再去推理,下结论;二是运用推理证明计算得出结论,或先利用条件特例得出结论,然后再根据条件给出证明或计算.本题第二问主要采用假设存在点,然后确定线面平行的性质进行求解. 本题第三问利用向量法求解二面角.
面面垂直.本题第一问利用方法二进行证明;探求某些点的具体位置,使得线面满足垂直关系,是一类逆向思维的题目.一般可采用两个方法:一是先假设存在,再去推理,下结论;二是运用推理证明计算得出结论,或先利用条件特例得出结论,然后再根据条件给出证明或计算.本题第二问主要采用假设存在点,然后确定线面平行的性质进行求解. 本题第三问利用向量法求解二面角.
练习册系列答案
相关题目
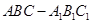 中,
中,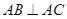 ,
,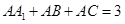 ,
,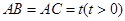 ,
,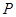 是侧棱
是侧棱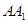 上的动点.
上的动点.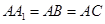 时,求证:
时,求证: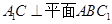 ;
; 的平面角的余弦值为
的平面角的余弦值为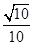 ,试求实数
,试求实数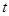 的值.
的值.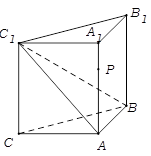
 ,侧面PAB是等边三角形,且侧面PAB⊥底面ABCD.
,侧面PAB是等边三角形,且侧面PAB⊥底面ABCD. 
 为平行四边形,
为平行四边形,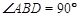 ,
,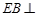 平面
平面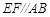 ,
,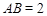 ,
, ,
,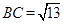 ,且
,且 是
是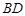 的中点.
的中点. 平面
平面 ;
;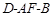 的大小;
的大小;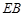 上是否存在一点
上是否存在一点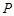 ,使得
,使得 与
与 所成的角为
所成的角为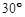 ? 若存在,求出
? 若存在,求出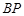 的长度;若不存在,请说明理由.
的长度;若不存在,请说明理由.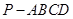 中,
中,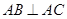 ,
,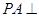 平面
平面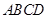 ,且
,且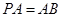 ,点
,点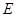 是
是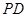 的中点.
的中点.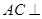 平面
平面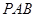 ;
; 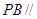 平面
平面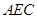
 ,有以下几个命题,其中是真命题的序号为 。(1)若
,有以下几个命题,其中是真命题的序号为 。(1)若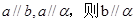 (2)
(2)
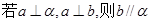 (4)
(4)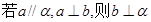
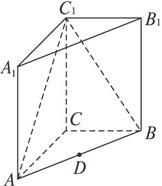
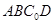 中,
中,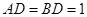 ,
,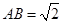 。沿它的对角线
。沿它的对角线 把△
把△ 折起,使点
折起,使点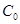 到达平面
到达平面 的位置。
的位置。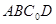 与平面
与平面 的位置关系,并给出证明;
的位置关系,并给出证明; 为等腰三角形,求此时二面角
为等腰三角形,求此时二面角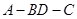 的大小。
的大小。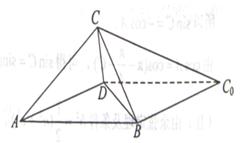
 中,底面
中,底面 是菱形,
是菱形, .
. ,求证:
,求证: 平面
平面 ;
; 平
平 面
面 ;
; 上是否存在点
上是否存在点 (异于点
(异于点 )使得
)使得 ∥平面
∥平面 ,若存在,求
,若存在,求 的值;若不存在,说明理由.
的值;若不存在,说明理由.