题目内容
如图,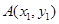 ,
,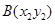 是抛物线
是抛物线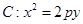 (
(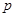 为正常数)上的两个动点,直线AB与x轴交于点P,与y轴交于点Q,且
为正常数)上的两个动点,直线AB与x轴交于点P,与y轴交于点Q,且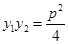
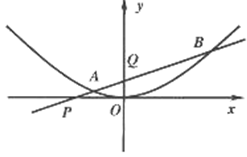
(Ⅰ)求证:直线AB过抛物线C的焦点;
(Ⅱ)是否存在直线AB,使得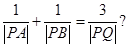 若存在,求出直线AB的方程;若不存在,请说明理由。
若存在,求出直线AB的方程;若不存在,请说明理由。
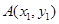 ,
,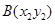 是抛物线
是抛物线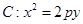 (
(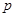 为正常数)上的两个动点,直线AB与x轴交于点P,与y轴交于点Q,且
为正常数)上的两个动点,直线AB与x轴交于点P,与y轴交于点Q,且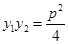

(Ⅰ)求证:直线AB过抛物线C的焦点;
(Ⅱ)是否存在直线AB,使得
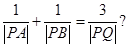 若存在,求出直线AB的方程;若不存在,请说明理由。
若存在,求出直线AB的方程;若不存在,请说明理由。(1)先求解直线AB的方程,来分析过定点。(2)直线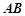 方程为
方程为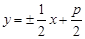
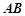 方程为
方程为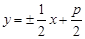
试题分析:(Ⅰ)由题意知,直线
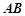 的斜率存在,且不为零.
的斜率存在,且不为零.设直线
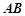 的方程为:
的方程为: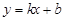 (
(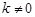 ,
,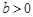 )
)由
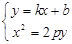 ,得
,得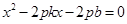 .∴
.∴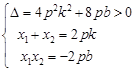 ,
, ∴

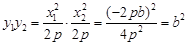 .
. ∵
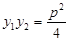 ,∴
,∴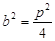 ,∵
,∵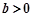 ,∴
,∴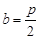 .
. ∴直线
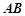 的方程为:
的方程为: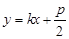 .
. 抛物线
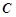 的焦点坐标为
的焦点坐标为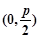 ,∴直线
,∴直线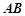 过抛物线C的焦点.
过抛物线C的焦点. (Ⅱ)假设存在直线
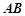 ,使得
,使得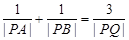 , 即
, 即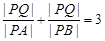 .
.作
 轴,
轴,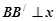 轴,垂足为
轴,垂足为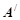 、
、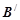 ,
,∴
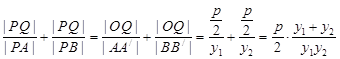
∵
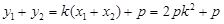 ,
, 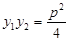
∴
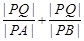 =
=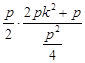 =
=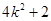 .
.由
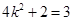 ,得
,得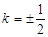 .
.故存在直线
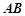 ,使得
,使得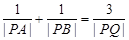 .直线
.直线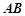 方程为
方程为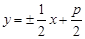 .
.点评:解决直线与抛物线的位置关系的运用问题,一般都要考查了抛物线的定义的运用,即抛物线上点到焦点的距离等于对其到准线的距离来解答,同时直线与抛物线的位置关系,也要结合设而不求的联立方程组的思想,结合韦达定理得到根与系数的关系,进而得到证明的结论,属于难度试题。

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
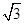
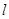 经过椭圆
经过椭圆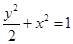 的焦点并且与椭圆相交于
的焦点并且与椭圆相交于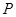 ,
,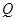 两点,线段
两点,线段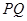 的垂直平分线与
的垂直平分线与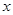 轴相交于点
轴相交于点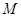 ,则
,则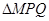 面积的最大值为 .
面积的最大值为 . 上的动点,点P在y轴上的射影是M,点A的坐标是
上的动点,点P在y轴上的射影是M,点A的坐标是 ,则
,则 的最小值是
的最小值是

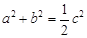 .则直线
.则直线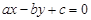 被圆
被圆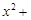
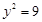 所截得的弦长为 .
所截得的弦长为 .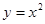 在点 处的切线平行于直线
在点 处的切线平行于直线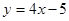 。
。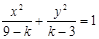 表示焦点在y轴上的椭圆,则k的取值范围是( )
表示焦点在y轴上的椭圆,则k的取值范围是( )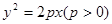 的焦点作一条直线交抛物线于
的焦点作一条直线交抛物线于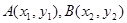 ,则
,则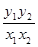 为( )
为( )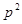
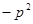
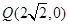 及抛物线
及抛物线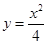 上的动点
上的动点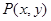 ,则
,则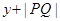 的最小值为______.
的最小值为______.