题目内容
过抛物线y2=2px(p>0)的焦点作倾斜角为30°的直线l与抛物线交于P,Q两点,分别作PP¢、QQ¢垂直于抛物线的准线于P¢、Q¢,若|PQ|=2,则四边形PP¢Q¢Q的面积为
| A.1 | B.2 | C.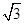 | D.3 |
A
试题分析:如图F(
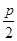 ,0),直线PQ方程为y=
,0),直线PQ方程为y= 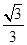 (x-
(x-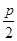 ),代入y2=2px整理得
),代入y2=2px整理得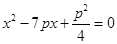 ,
,设
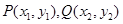 ,则
,则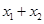 ="7p,"
="7p," 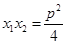 ,
,所以
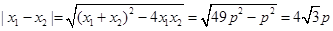 ,
,由
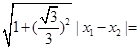 2,得
2,得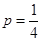 。所以梯形的高为
。所以梯形的高为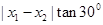 =
=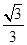 ×
×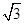 =1,故四边形PP¢Q¢Q的面积为
=1,故四边形PP¢Q¢Q的面积为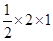 =1,故选A。
=1,故选A。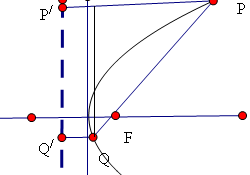
点评:中档题,所得四边形是梯形,且上下底边和为PQ=2,因此,只需求梯形的高。通过联立方程组,应用韦达定理、弦长公式,达到解题目的。

练习册系列答案
相关题目
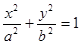 (
(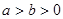 ),点
),点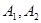 为椭圆C的左、右顶点。
为椭圆C的左、右顶点。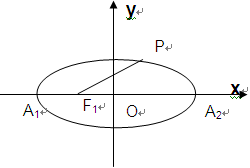
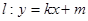 与(1)中所述椭圆C相交于A、B两点(A、B不是左、右顶点),且满足
与(1)中所述椭圆C相交于A、B两点(A、B不是左、右顶点),且满足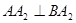 ,求证:直线
,求证:直线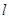 过定点,并求出该点的坐标。
过定点,并求出该点的坐标。 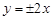 的是
的是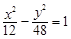
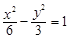
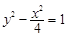
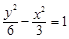
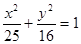 的左右焦点为
的左右焦点为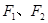 ,弦
,弦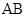 过点
过点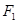 ,若△
,若△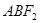 的内切圆周长为
的内切圆周长为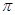 ,点
,点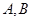 坐标分别为
坐标分别为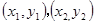 ,则
,则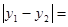 。
。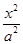 +
+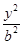 =1(a>b>0)的一个焦点是圆x2+y2-6x+8=0的圆心,且短轴长为8,则椭圆的左顶点为( )
=1(a>b>0)的一个焦点是圆x2+y2-6x+8=0的圆心,且短轴长为8,则椭圆的左顶点为( ) 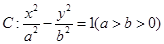 的右焦点为
的右焦点为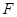 ,左右顶点分别为
,左右顶点分别为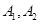 ,过
,过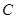 的一条渐近线平行的直线
的一条渐近线平行的直线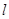 与另一条渐近线相交于
与另一条渐近线相交于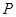 ,若
,若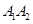 为直径的圆上,则双曲线的离心率为________ ______.
为直径的圆上,则双曲线的离心率为________ ______.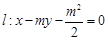 ,椭圆C:
,椭圆C: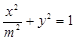 ,
,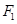 、
、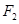 分别为椭圆C的左、右焦点.
分别为椭圆C的左、右焦点.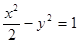 有相同的渐近线的双曲线方程是( )
有相同的渐近线的双曲线方程是( )

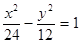
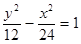
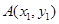 ,
,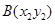 是抛物线
是抛物线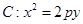 (
(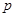 为正常数)上的两个动点,直线AB与x轴交于点P,与y轴交于点Q,且
为正常数)上的两个动点,直线AB与x轴交于点P,与y轴交于点Q,且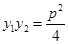
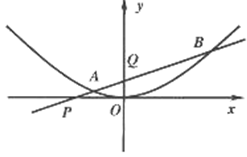
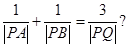 若存在,求出直线AB的方程;若不存在,请说明理由。
若存在,求出直线AB的方程;若不存在,请说明理由。