题目内容
在△ABC中,角A,B,C的对边分别a,b,c,若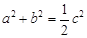 .则直线
.则直线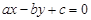 被圆
被圆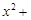
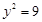 所截得的弦长为 .
所截得的弦长为 .
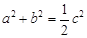 .则直线
.则直线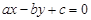 被圆
被圆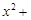
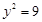 所截得的弦长为 .
所截得的弦长为 .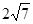
试题分析:由半径、弦的一半、圆心距所确定的“特征直角三角形”及
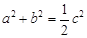 得,
得,直线
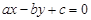 被圆
被圆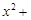
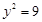 所截得的弦长为2
所截得的弦长为2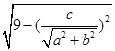 =
=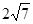 。
。点评:典型题,涉及直线被圆截得弦长问题,往往要借助于半径、弦的一半、圆心距所确定的“特征直角三角形”。

练习册系列答案
相关题目
题目内容
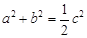 .则直线
.则直线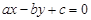 被圆
被圆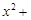
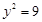 所截得的弦长为 .
所截得的弦长为 .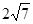
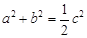 得,
得,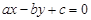 被圆
被圆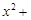
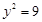 所截得的弦长为2
所截得的弦长为2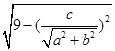 =
=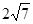 。
。