题目内容
(本题12分)在数列{an}中,a1=2,an+1="4" an-3n+1,n∈N*.
(1)证明数列{an-n}是等比数列;(2)求数列{an}的前n项和Sn;(3)证明不等式Sn+1≤4Sn,对任意n∈N*皆成立。
(1)证明数列{an-n}是等比数列;(2)求数列{an}的前n项和Sn;(3)证明不等式Sn+1≤4Sn,对任意n∈N*皆成立。
(Ⅰ)见解析 (Ⅱ) S n= (Ⅲ)见解析
(Ⅲ)见解析
 (Ⅲ)见解析
(Ⅲ)见解析(1)证明:由题设an+1="4" an-3n+1,得an+1 _(n+1)="4" (an-n), n∈N*,
又a1-1=1,所以数列{ an-n }是首项为1,且公比为4的等比数列。
(2)由(1)可知an - n="4" n-1,于是数列{ an}的通项公式为an=" 4" n-1+n,
所以数列{an}的前n项和为S n= 。
。
(3)证明:对任意的n∈N*,

 。
。
∵对任意n∈N*, ,∴
,∴ ,
,
所以不等式Sn+1≤4Sn,对任意n∈N*皆成立。
又a1-1=1,所以数列{ an-n }是首项为1,且公比为4的等比数列。
(2)由(1)可知an - n="4" n-1,于是数列{ an}的通项公式为an=" 4" n-1+n,
所以数列{an}的前n项和为S n=
 。
。(3)证明:对任意的n∈N*,

 。
。∵对任意n∈N*,
 ,∴
,∴ ,
,所以不等式Sn+1≤4Sn,对任意n∈N*皆成立。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 过曲线
过曲线 上一点
上一点 ,斜率为
,斜率为 ,且
,且 ,其中
,其中
 表示
表示 ;
; ;
;  对
对 恒成立,求实数a的取值范围。
恒成立,求实数a的取值范围。 中,
中, ,数列
,数列 满足
满足 ,且
,且 (1)求数列
(1)求数列 的前
的前 项的和
项的和 .
. 为等差数列
为等差数列 的前
的前 项和,且
项和,且 ,
, ,则
,则 ( )
( )


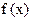 ,若存在
,若存在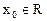 ,使
,使 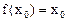 成立,则称
成立,则称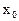 为
为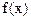 的“滞点”.已知函数f ( x ) =
的“滞点”.已知函数f ( x ) = 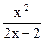 .
.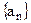 的各项均为负数,且满足
的各项均为负数,且满足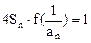 ,求数列
,求数列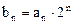 ,求
,求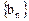 的前项和
的前项和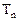 .
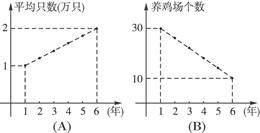
.

 ;
;