题目内容
直线 过曲线
过曲线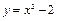 上一点
上一点 ,斜率为
,斜率为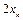 ,且
,且 与x轴交于点
与x轴交于点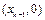 ,其中
,其中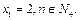
⑴试用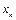 表示
表示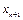 ;
;
⑵证明: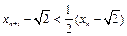 ;
;
⑶若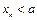 对
对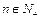 恒成立,求实数a的取值范围。
恒成立,求实数a的取值范围。
 过曲线
过曲线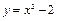 上一点
上一点 ,斜率为
,斜率为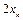 ,且
,且 与x轴交于点
与x轴交于点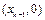 ,其中
,其中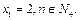
⑴试用
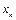 表示
表示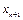 ;
;⑵证明:
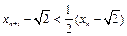 ;
; ⑶若
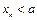 对
对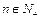 恒成立,求实数a的取值范围。
恒成立,求实数a的取值范围。(1)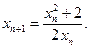 (2)证明见解析(3)
(2)证明见解析(3)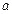 的取值范围是
的取值范围是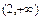 .
.
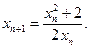 (2)证明见解析(3)
(2)证明见解析(3)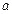 的取值范围是
的取值范围是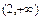 .
.(1)依题意得直线
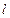 的方程为
的方程为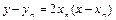 ,令
,令 ,即
,即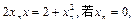 则直线
则直线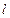 的方程为
的方程为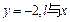 轴无交点,
轴无交点,故
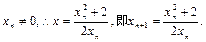
(2)
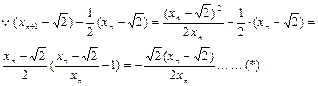
由于
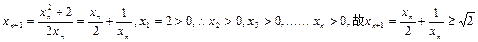
又若
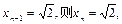 从而
从而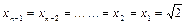 ,这与
,这与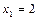 矛盾,
矛盾,因此
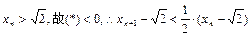
(3)
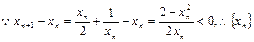 单调递减,
单调递减,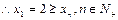 恒成立,则只需
恒成立,则只需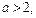 故
故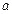 的取值范围是
的取值范围是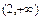 .
. 
练习册系列答案
相关题目
 ≥2,用
≥2,用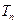 表示关于
表示关于 的一元二次方程
的一元二次方程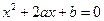 有实数根的有序数组
有实数根的有序数组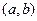 的组数,其中
的组数,其中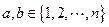 (
(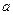 和
和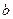 可以相等);对于随机选取的
可以相等);对于随机选取的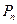 为关于
为关于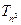 和
和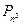 ;
;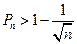 。
。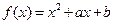 (
(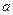 、
、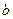 为实常数),已知不等式
为实常数),已知不等式
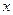 均成立.定义数列
均成立.定义数列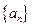 和
和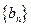 :
: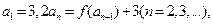
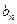 =
=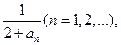 数列
数列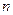 项和
项和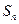 .
.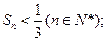
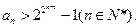
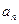 ;(Ⅱ)求{an}前n项和Sn的最大值.
;(Ⅱ)求{an}前n项和Sn的最大值.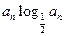 ,sn=b1+b2+┉+bn,对任意正整数n,sn+(n+m)an+1<0恒成立,试求m的取值范围。
,sn=b1+b2+┉+bn,对任意正整数n,sn+(n+m)an+1<0恒成立,试求m的取值范围。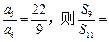 ______________.
______________.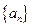 的前
的前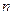 和为
和为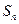 ,且有
,且有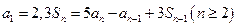
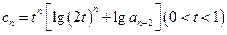 ,且数列
,且数列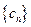 中的每一项总小于它后面的项,求实数
中的每一项总小于它后面的项,求实数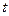 的取值范围。
的取值范围。