题目内容
3.集合M={x|x2-2x-3<0},N={x|x2+x+1>0},则M∩N是( )| A. | (-3,1) | B. | R | C. | (-1,3) | D. | ∅ |
分析 求出集合的等价条件,利用集合的基本运算进行求解即可.
解答 解:M={x|x2-2x-3<0}={x|-1<x<3},
N={x|x2+x+1>0}=R,
则M∩N={x|-1<x<3}=(-1,3),
故选:C.
点评 本题主要考查集合的基本运算,根据条件求出集合的等价条件是解决本题的关键.

练习册系列答案
相关题目
11. 如图,一隧道截面由一个长方形和抛物线构成,现欲在隧道抛物线拱顶上安装交通信息采集装置,若位置C对隧道底AB的张角θ最大时采集效果最好,则采集效果最好时位置C到AB的距离是( )
如图,一隧道截面由一个长方形和抛物线构成,现欲在隧道抛物线拱顶上安装交通信息采集装置,若位置C对隧道底AB的张角θ最大时采集效果最好,则采集效果最好时位置C到AB的距离是( )
 如图,一隧道截面由一个长方形和抛物线构成,现欲在隧道抛物线拱顶上安装交通信息采集装置,若位置C对隧道底AB的张角θ最大时采集效果最好,则采集效果最好时位置C到AB的距离是( )
如图,一隧道截面由一个长方形和抛物线构成,现欲在隧道抛物线拱顶上安装交通信息采集装置,若位置C对隧道底AB的张角θ最大时采集效果最好,则采集效果最好时位置C到AB的距离是( )| A. | 2$\sqrt{2}$m | B. | 2$\sqrt{3}$m | C. | 4m | D. | 6m |
15.设F1、F2分别是椭圆$\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{16}$=1的左、焦点,P为椭圆上一点,M是F1P的中点,|OM|=3,则P点到椭圆左焦点的距离为( )
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
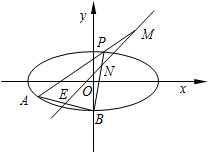 如图,已知椭圆$C:\frac{x^2}{12}+\frac{y^2}{4}=1$,点B是其下顶点,过点B的直线交椭圆C于另一点A(A点在x轴下方),且线段AB的中点E在直线y=x上.
如图,已知椭圆$C:\frac{x^2}{12}+\frac{y^2}{4}=1$,点B是其下顶点,过点B的直线交椭圆C于另一点A(A点在x轴下方),且线段AB的中点E在直线y=x上.