题目内容
13.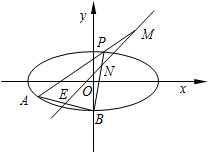 如图,已知椭圆$C:\frac{x^2}{12}+\frac{y^2}{4}=1$,点B是其下顶点,过点B的直线交椭圆C于另一点A(A点在x轴下方),且线段AB的中点E在直线y=x上.
如图,已知椭圆$C:\frac{x^2}{12}+\frac{y^2}{4}=1$,点B是其下顶点,过点B的直线交椭圆C于另一点A(A点在x轴下方),且线段AB的中点E在直线y=x上.(1)求直线AB的方程;
(2)若点P为椭圆C上异于A、B的动点,且直线AP,BP分别交直线y=x于点M、N,证明:OM•ON为定值.
分析 (1)设点E(m,m),则A(2m,2m+2),通过将点A代入椭圆C,计算即得结论;
(2)设P(x0,y0),分别联立直线AP与直线y=x的方程、直线BP与直线y=x的方程,计算即得结论.
解答 (1)解:设点E(m,m),∵B(0,-2),∴A(2m,2m+2),
∵点A在椭圆C上,∴$\frac{4{m}^{2}}{12}+\frac{(2m+2)^{2}}{4}=1$,
解得m=-$\frac{3}{2}$或m=0(舍去),
∴A(-3,-1),
∴直线AB的方程为:x+3y+6=0;
(2)证明:设P(x0,y0),则$\frac{{{x}_{0}}^{2}}{12}+\frac{{{y}_{0}}^{2}}{4}=1$,
①直线AP方程为:y+1=$\frac{{y}_{0}+1}{{x}_{0}+3}$(x+3),
联立直线AP与直线y=x的方程,解得:xM=$\frac{3{y}_{0}-{x}_{0}}{{x}_{0}-{y}_{0}+2}$,
同理xN=$\frac{-2{x}_{0}}{{x}_{0}-{y}_{0}-2}$,
∴OM•ON=$\sqrt{2}$|xM|•$\sqrt{2}$|xN|=2|$\frac{3{y}_{0}-{x}_{0}}{{x}_{0}-{y}_{0}+2}$•$\frac{-2{x}_{0}}{{x}_{0}-{y}_{0}-2}$|=2|$\frac{{{x}_{0}}^{2}-3{x}_{0}{y}_{0}}{\frac{{{x}_{0}}^{2}}{3}-{x}_{0}{y}_{0}}$|=6
点评 本题是一道直线与圆锥曲线的综合题,考查求直线的方程、线段乘积为定值等问题,考查运算求解能力,注意解题方法的积累,属于中档题.

解:由ax2+bx+c>0的解集为(1,2),得,a($\frac{1}{x}$)2+b($\frac{1}{x}$)+c>0的解集为($\frac{1}{2}$,1),
即关于x的不等式cx2+bx+a>0的解集为($\frac{1}{2}$,1).
参考上述解法:若关于x的不等式$\frac{b}{x+a}$+$\frac{x+b}{x+c}$<0的解集为(-1,-$\frac{1}{3}$)∪($\frac{1}{2}$,1),则关于x的不等式$\frac{b}{x-a}$-$\frac{x-b}{x-c}$>0的解集为( )
| A. | (-1,1) | B. | (-1,-$\frac{1}{2}$)∪($\frac{1}{3}$,1) | C. | (-∞,-$\frac{1}{2}$)∪($\frac{1}{3}$,1) | D. | (-∞,-$\frac{1}{2}$)∪($\frac{1}{3}$,+∞) |

| A. | $\frac{{470+10\sqrt{30}}}{3}$ | B. | 175 | C. | 180 | D. | 295+10$\sqrt{2}$ |
| A. | (-3,1) | B. | R | C. | (-1,3) | D. | ∅ |