题目内容
13.(1)已知数列an=-n2+13.6n,则当n=7时an取得最大值;(2)已知a7是数列an=-n2+λn唯一的最大值,则实数λ的取值范围是13<λ<15.
分析 (1)化简an=-n2+13.6n=-(n-6.8)2+6.82,由二次函数的性质可判断;
(2)化简an=-n2+λn=-(n-$\frac{λ}{2}$)2+($\frac{λ}{2}$)2,由二次函数的性质可判断.
解答 解:(1)∵an=-n2+13.6n=-(n-6.8)2+6.82,
故当n=7时,an取得最大值;
(2)an=-n2+λn=-(n-$\frac{λ}{2}$)2+($\frac{λ}{2}$)2,
∵a7是数列an=-n2+λn唯一的最大值,
∴6.5<$\frac{λ}{2}$<7.5;
∴13<λ<15;
故答案为:(1)7,(2)13<λ<15.
点评 本题考查了数列的函数特性,同时考查了二次函数的性质,属于基础题.

练习册系列答案
 能力评价系列答案
能力评价系列答案
相关题目
3.集合M={x|x2-2x-3<0},N={x|x2+x+1>0},则M∩N是( )
| A. | (-3,1) | B. | R | C. | (-1,3) | D. | ∅ |
4.国务院召开青少年校园足球工作电视电话会议,提出教育部将主导校园足球“足球进校园”活动.某市教育部门未了解学生喜欢足球是否与性别有关,在某学校该校50名学生进行了问卷调查,得到了如下的列联表:
(Ⅰ)按性别用分层抽样的方法在喜欢足球的学生中抽取6人,求这6人中男生的人数;
(Ⅱ)在上述抽取的6人中随机抽取2人做进一步调查,求恰有1名女生的概率;
(Ⅲ)根据列联表的独立性检验,能否在犯错误的概率不超过0.01的前提下,认为喜欢足球与性别有关系?
下面的临界值表供参考:
(参考公式:${K}^{2}=\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$,其中n=a+b+c+d)
| 喜欢足球 | 不喜欢足球 | 合计 | |
| 男生 | 20 | 5 | 25 |
| 女生 | 10 | 15 | 25 |
| 合计 | 30 | 20 | 50 |
(Ⅱ)在上述抽取的6人中随机抽取2人做进一步调查,求恰有1名女生的概率;
(Ⅲ)根据列联表的独立性检验,能否在犯错误的概率不超过0.01的前提下,认为喜欢足球与性别有关系?
下面的临界值表供参考:
| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| K | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
5.已知函数f(x)是定义在R上的偶函数,且在区间[0,+∞)上为减函数,若$f({ln\frac{n}{m}})$+$f({ln\frac{m}{n}})$-2f(1)>0,则$\frac{{{m^2}+{n^2}}}{mn}$的取值范围是( )
| A. | (e,+∞) | B. | [2,e) | C. | $({e+\frac{1}{e},+∞})$ | D. | $[{2,e+\frac{1}{e}})$ |
2.执行如图的程序框图,如果输入a=4,那么输出的n的值为( )
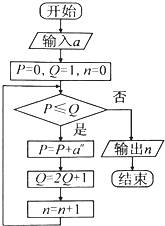

| A. | 5 | B. | 4 | C. | 3 | D. | 2 |
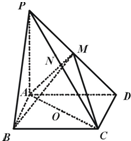 如图,在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,PA=AD=4,AB=2.若M,N分别为棱PD,PC上的点,O为AC的中点,且AC=2OM=2ON.
如图,在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,PA=AD=4,AB=2.若M,N分别为棱PD,PC上的点,O为AC的中点,且AC=2OM=2ON.