题目内容
18.化简求值:(1)sin$\frac{π}{12}$-$\sqrt{3}$cos$\frac{π}{12}$;
(2)$\frac{sin15°-cos15°}{cos15°+sin15°}$.
分析 (1)由两角差的正弦函数公式化简后即可求值.
(2)由倍角公式及特殊角的三角函数值即可求值.
解答 解:(1)sin$\frac{π}{12}$-$\sqrt{3}$cos$\frac{π}{12}$=2×($\frac{1}{2}$sin$\frac{π}{12}$-$\frac{\sqrt{3}}{2}$cos$\frac{π}{12}$)=2sin($\frac{π}{12}-\frac{π}{3}$)=-2sin$\frac{π}{4}$=-$\sqrt{2}$.
(2)$\frac{sin15°-cos15°}{cos15°+sin15°}$=$\frac{-(cos15°-sin15°)^{2}}{co{s}^{2}15°-si{n}^{2}15°}$=$\frac{-(1-sin30°)}{cos30°}$=-$\frac{\sqrt{3}}{3}$.
点评 本题主要考查了两角差的正弦函数公式,倍角公式及特殊角的三角函数值的应用,熟练记忆相关公式是解题的关键,属于基础题.

练习册系列答案
相关题目
3.集合M={x|x2-2x-3<0},N={x|x2+x+1>0},则M∩N是( )
| A. | (-3,1) | B. | R | C. | (-1,3) | D. | ∅ |
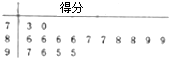 钓鱼岛及其附近海域自古以来就是中国人民进行捕鱼、避风、休息的场所,被誉为深海中的翡翠.某学校就钓鱼岛有关常识随机抽取了16名学生进行测试,用“10分制”以茎叶图方式记录了他们对钓鱼岛的了解程度,分数以小数点前的一位数字为茎,小数点后的一位数字为叶.
钓鱼岛及其附近海域自古以来就是中国人民进行捕鱼、避风、休息的场所,被誉为深海中的翡翠.某学校就钓鱼岛有关常识随机抽取了16名学生进行测试,用“10分制”以茎叶图方式记录了他们对钓鱼岛的了解程度,分数以小数点前的一位数字为茎,小数点后的一位数字为叶.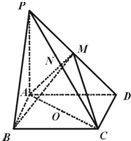 如图,在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,PA=AD=4,AB=2.若M,N分别为棱PD,PC上的点,O为AC的中点,且AC=2OM=2ON.
如图,在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,PA=AD=4,AB=2.若M,N分别为棱PD,PC上的点,O为AC的中点,且AC=2OM=2ON.