题目内容
8.已知cn=(3n-1)$\frac{2}{{3}^{n}}$,n=1,2,3,…,Tn为数列{cn}的前n项和,求Tn.分析 利用“错位相减法”、等比数列的前n项和公式即可得出.
解答 解:∵cn=(3n-1)$\frac{2}{{3}^{n}}$,
∴数列{cn}的前n项和Tn=$2(\frac{2}{3}+\frac{5}{{3}^{2}}+\frac{8}{{3}^{3}}$+…+$\frac{3n-1}{{3}^{n}})$,
$\frac{1}{3}{T}_{n}$=2$(\frac{2}{{3}^{2}}+\frac{5}{{3}^{3}}+…+\frac{3n-4}{{3}^{n}}+\frac{3n-1}{{3}^{n+1}})$,
∴$\frac{2}{3}{T}_{n}$=2$(\frac{2}{3}+\frac{3}{{3}^{2}}+\frac{3}{{3}^{3}}+$…+$\frac{3}{{3}^{n}}-\frac{3n-1}{{3}^{n+1}})$,
∴Tn=2+$\frac{3}{3}+\frac{3}{{3}^{2}}$+…+$\frac{3}{{3}^{n-1}}$-$\frac{3n-1}{{3}^{n}}$=3×$\frac{1-\frac{1}{{3}^{n}}}{1-\frac{1}{3}}$-1-$\frac{3n-1}{{3}^{n}}$=$\frac{7}{2}-\frac{6n+7}{2×{3}^{n}}$.
∴Tn=$\frac{7}{2}-\frac{6n+7}{2×{3}^{n}}$.
点评 本题考查了“错位相减法”、等比数列的前n项和公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
3.集合M={x|x2-2x-3<0},N={x|x2+x+1>0},则M∩N是( )
| A. | (-3,1) | B. | R | C. | (-1,3) | D. | ∅ |
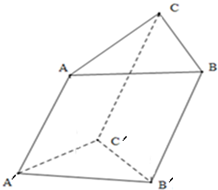 斜三棱柱底面边长是4cm的正三角形,.侧棱长3cm,侧棱∠AA′C′=∠AA′B′=60°.
斜三棱柱底面边长是4cm的正三角形,.侧棱长3cm,侧棱∠AA′C′=∠AA′B′=60°.