题目内容
设a为正实数,函数f(x)=x3-ax2-a2x+1, x∈R.
(1)求f(x)的极值;
(2)设曲线y=f(x)与直线y=0至多有两个公共点,求实数a的取值范围.
(1)求f(x)的极值;
(2)设曲线y=f(x)与直线y=0至多有两个公共点,求实数a的取值范围.
(1)f(x)(极大)=f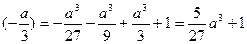
f(x)(极小)=f(a)=a3-a3-a3+1=1-a3
(2)见解析(3)0<a≤1
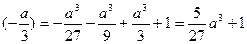
f(x)(极小)=f(a)=a3-a3-a3+1=1-a3
(2)见解析(3)0<a≤1
(1)f′(x)=3x2-2ax-a2……………………………………………………2分
由f′(x)=3x2-2ax-a2=0,得x1=-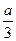 ,x2="a," (a>0)
,x2="a," (a>0)
……………………………………………………………………………………5分
∴f(x)(极大)=f
f(x)(极小)=f(a)=a3-a3-a3+1=1-a3……………………………………………7分
(2)∵f(x)在(-∞,-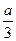 )上递增,在(-
)上递增,在(-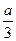 ,a)上递减,在(a,+ ∞)上递增,
,a)上递减,在(a,+ ∞)上递增,
f(x)(极大)=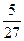 a3+1>0………………………………………………………………9分
a3+1>0………………………………………………………………9分
①当极小值f(a)=1-a3≥0,即0<a≤1时,y=f(x)与y=0在x∈(-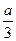 ,+∞)上有1个或0个公共点,此时f(-1)=a(a-1) ≤0
,+∞)上有1个或0个公共点,此时f(-1)=a(a-1) ≤0
∴y=f(x)与y="0 " 在x∈(-∞,-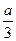 )上有1个公共点
)上有1个公共点
∴0<a≤1时,y=f(x)与y=0有1个或2个公共点……………………………11分
②当极小值f(a)=1-a3<0即a>1时,y=f(x)与y=0在x∈(-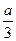 ,+∞)上有2个公共点,此时f(-a)=1-a3<0
,+∞)上有2个公共点,此时f(-a)=1-a3<0
∴y=f(x)与y="0" 在x∈(-∞,-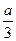 )上有1个公共点
)上有1个公共点
∴a>1时,y=f(x)与y=0有3个公共点………………………………………13分
综上,0<a≤1……………………………………………………………………14分
由f′(x)=3x2-2ax-a2=0,得x1=-
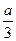 ,x2="a," (a>0)
,x2="a," (a>0)| x | (-,-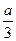 ) ) | -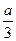 | (-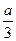 ,a) ,a) | a | (a,+ ∞) |
| f′(x) | + | 0 | - | 0 | + |
| f(x) | 增 | 极大 | 减 | 极小 | 增 |
∴f(x)(极大)=f

f(x)(极小)=f(a)=a3-a3-a3+1=1-a3……………………………………………7分
(2)∵f(x)在(-∞,-
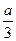 )上递增,在(-
)上递增,在(-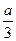 ,a)上递减,在(a,+ ∞)上递增,
,a)上递减,在(a,+ ∞)上递增,f(x)(极大)=
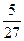 a3+1>0………………………………………………………………9分
a3+1>0………………………………………………………………9分①当极小值f(a)=1-a3≥0,即0<a≤1时,y=f(x)与y=0在x∈(-
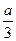 ,+∞)上有1个或0个公共点,此时f(-1)=a(a-1) ≤0
,+∞)上有1个或0个公共点,此时f(-1)=a(a-1) ≤0∴y=f(x)与y="0 " 在x∈(-∞,-
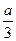 )上有1个公共点
)上有1个公共点∴0<a≤1时,y=f(x)与y=0有1个或2个公共点……………………………11分
②当极小值f(a)=1-a3<0即a>1时,y=f(x)与y=0在x∈(-
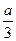 ,+∞)上有2个公共点,此时f(-a)=1-a3<0
,+∞)上有2个公共点,此时f(-a)=1-a3<0∴y=f(x)与y="0" 在x∈(-∞,-
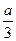 )上有1个公共点
)上有1个公共点∴a>1时,y=f(x)与y=0有3个公共点………………………………………13分
综上,0<a≤1……………………………………………………………………14分

练习册系列答案
 快乐5加2金卷系列答案
快乐5加2金卷系列答案
相关题目
 的图象上以N(1,n)为切点的切线的倾斜角为
的图象上以N(1,n)为切点的切线的倾斜角为
 恒成立?如果存在,请求出最小的正整数k;如果不存在,请说明理由;
恒成立?如果存在,请求出最小的正整数k;如果不存在,请说明理由;
 ,且函数
,且函数 的图象关于原点对称,其图象在
的图象关于原点对称,其图象在 处的切线方程为
处的切线方程为 (1)求
(1)求 使得函数
使得函数 的定义域和值域均为
的定义域和值域均为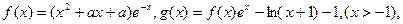
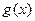 的单调区间,并证明此时方程
的单调区间,并证明此时方程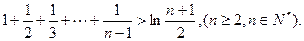
 =
= 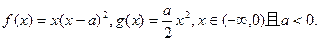
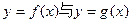 的图象的交点A的坐标;
的图象的交点A的坐标;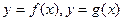 的图象在交点A处的切线分别为
的图象在交点A处的切线分别为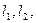 是否存在这样的实数a,使得
是否存在这样的实数a,使得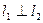 ?若存在,请求出a的值和相应的点A坐标;若不存在,请说明理由。
?若存在,请求出a的值和相应的点A坐标;若不存在,请说明理由。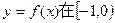 上最小值为F(a),求
上最小值为F(a),求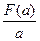 的最小值。
的最小值。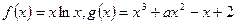
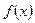 的单调区间;
的单调区间;
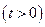 上的最小值;
上的最小值;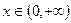 ,
,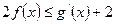 恒成立,求实数
恒成立,求实数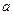 的取值范围.
的取值范围. 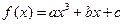
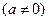 为奇函数,其图象在点
为奇函数,其图象在点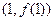 处的切线与直线
处的切线与直线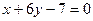 垂直,且在x=-1处取得极值.
垂直,且在x=-1处取得极值.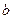 ,
,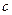 的值;
的值;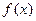 在
在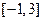 上的最大值和最小值。
上的最大值和最小值。