题目内容
设函数 .
.
(1)若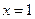 是函数
是函数 的一个极值点,试求出
的一个极值点,试求出 关于
关于 的关系式(用
的关系式(用 表示
表示 ),并确定
),并确定 的单调区间;
的单调区间;
(2)在(1)的条件下,设 ,函数
,函数 .若存在
.若存在 使得
使得 成立,求
成立,求 的取值范围.
的取值范围.
 .
.(1)若
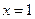 是函数
是函数 的一个极值点,试求出
的一个极值点,试求出 关于
关于 的关系式(用
的关系式(用 表示
表示 ),并确定
),并确定 的单调区间;
的单调区间;(2)在(1)的条件下,设
 ,函数
,函数 .若存在
.若存在 使得
使得 成立,求
成立,求 的取值范围.
的取值范围.:当 时,函数
时,函数 的单调递增区间为
的单调递增区间为 和
和 ,单调递减区间为
,单调递减区间为 ;当
;当 时,函数
时,函数 单调递增区间为
单调递增区间为 和
和 ,单调递减区间为
,单调递减区间为

 时,函数
时,函数 的单调递增区间为
的单调递增区间为 和
和 ,单调递减区间为
,单调递减区间为 ;当
;当 时,函数
时,函数 单调递增区间为
单调递增区间为 和
和 ,单调递减区间为
,单调递减区间为

解:(1)∵ =
= -------1分
-------1分
且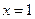 是函数
是函数 的一个极值点 ∴
的一个极值点 ∴ -------------------------------------------2分
-------------------------------------------2分
即 ,解得
,解得 -------------3分
-------------3分
则 =
=
令 ,得
,得 或
或 ------------------------4分
------------------------4分
∵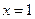 是极值点,∴
是极值点,∴ ,即
,即
当 即
即 时,由
时,由 得
得 或
或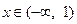
由 得
得 -------------------------------------5分
-------------------------------------5分
当 即
即 时,由
时,由 得
得 或
或
由 得
得 -------------------------------------6分
-------------------------------------6分
综上可知:当 时,函数
时,函数 的单调递增区间为
的单调递增区间为 和
和 ,单调递减区间为
,单调递减区间为 ;当
;当 时,函数
时,函数 单调递增区间为
单调递增区间为 和
和 ,单调递减区间为
,单调递减区间为 ------------------8分
------------------8分
(2)由(1)知,当a>0时, 在区间(0,1)上的单调递减,在区间(1,4)上单调递增,
在区间(0,1)上的单调递减,在区间(1,4)上单调递增,
∴函数 在区间
在区间 上的最小值为
上的最小值为 ----------------------------------9分
----------------------------------9分
又∵

 ,
, ,
,
∴函数 在区间[0,4]上的值域是
在区间[0,4]上的值域是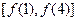 ,即
,即 --------------11分
--------------11分
又 在区间[0,4]上是增函数,
在区间[0,4]上是增函数,
且它在区间[0,4]上的值域是 --------------------------------------------12分
--------------------------------------------12分
∵ -
- =
= =
= ,
,
∴存在 使得
使得 成立只须仅须
成立只须仅须
 -
- <1
<1
 .--------14分
.--------14分
 =
= -------1分
-------1分且
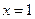 是函数
是函数 的一个极值点 ∴
的一个极值点 ∴ -------------------------------------------2分
-------------------------------------------2分即
 ,解得
,解得 -------------3分
-------------3分则
 =
=
令
 ,得
,得 或
或 ------------------------4分
------------------------4分∵
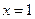 是极值点,∴
是极值点,∴ ,即
,即
当
 即
即 时,由
时,由 得
得 或
或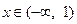
由
 得
得 -------------------------------------5分
-------------------------------------5分当
 即
即 时,由
时,由 得
得 或
或
由
 得
得 -------------------------------------6分
-------------------------------------6分综上可知:当
 时,函数
时,函数 的单调递增区间为
的单调递增区间为 和
和 ,单调递减区间为
,单调递减区间为 ;当
;当 时,函数
时,函数 单调递增区间为
单调递增区间为 和
和 ,单调递减区间为
,单调递减区间为 ------------------8分
------------------8分(2)由(1)知,当a>0时,
 在区间(0,1)上的单调递减,在区间(1,4)上单调递增,
在区间(0,1)上的单调递减,在区间(1,4)上单调递增,∴函数
 在区间
在区间 上的最小值为
上的最小值为 ----------------------------------9分
----------------------------------9分又∵


 ,
, ,
,∴函数
 在区间[0,4]上的值域是
在区间[0,4]上的值域是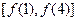 ,即
,即 --------------11分
--------------11分又
 在区间[0,4]上是增函数,
在区间[0,4]上是增函数,且它在区间[0,4]上的值域是
 --------------------------------------------12分
--------------------------------------------12分∵
 -
- =
= =
= ,
,∴存在
 使得
使得 成立只须仅须
成立只须仅须 -
- <1
<1
 .--------14分
.--------14分
练习册系列答案
 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案
相关题目
 的图象上以N(1,n)为切点的切线的倾斜角为
的图象上以N(1,n)为切点的切线的倾斜角为
 恒成立?如果存在,请求出最小的正整数k;如果不存在,请说明理由;
恒成立?如果存在,请求出最小的正整数k;如果不存在,请说明理由;
 .
. 时,求
时,求 的单调区间和极值;
的单调区间和极值; ,
, 恒成立,求
恒成立,求 的取值范围.
的取值范围. ,函数
,函数 ,
, .
. 的单调性
的单调性 ,求证:
,求证: 有三个不同的实根.
有三个不同的实根.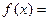
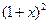 -4
-4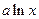 (a∈N﹡).(Ⅰ)若函数
(a∈N﹡).(Ⅰ)若函数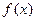 在(1,+∞)上是增函数,求a的值;(Ⅱ)在(Ⅰ)的条件下,若关于x的方程
在(1,+∞)上是增函数,求a的值;(Ⅱ)在(Ⅰ)的条件下,若关于x的方程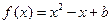 在区间[1,e]上恰有一个实根,求实数b的取值范围.
在区间[1,e]上恰有一个实根,求实数b的取值范围. 函数
函数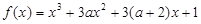 有极值;命题
有极值;命题 函数
函数 且
且 恒成立.若
恒成立.若 为真命题,
为真命题, 为真命题,则
为真命题,则 的取值范围是
的取值范围是




 =
= 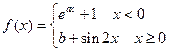 在R上可导,则
在R上可导,则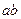 =" " ( )
=" " ( ) ,则
,则 ( )
( )


