题目内容
设函数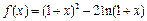 .
.
(Ⅰ)求f (x)的单调区间;
(Ⅱ)若当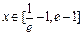 时,不等式f (x)<m恒成立,求实数m的取值范围;
时,不等式f (x)<m恒成立,求实数m的取值范围;
(Ⅲ)若关于x的方程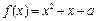 在区间[0, 2]上恰好有两个相异的实根,求实数a的取值范围.
在区间[0, 2]上恰好有两个相异的实根,求实数a的取值范围.
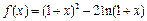 .
.(Ⅰ)求f (x)的单调区间;
(Ⅱ)若当
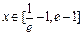 时,不等式f (x)<m恒成立,求实数m的取值范围;
时,不等式f (x)<m恒成立,求实数m的取值范围;(Ⅲ)若关于x的方程
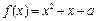 在区间[0, 2]上恰好有两个相异的实根,求实数a的取值范围.
在区间[0, 2]上恰好有两个相异的实根,求实数a的取值范围.(Ⅰ)f (x)的递增区间是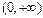 ,递减区间是(-1, 0)
,递减区间是(-1, 0)
(Ⅱ)当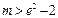 时,不等式f (x)<m恒成立.(Ⅲ)a的取值范围是
时,不等式f (x)<m恒成立.(Ⅲ)a的取值范围是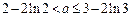
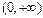 ,递减区间是(-1, 0)
,递减区间是(-1, 0)(Ⅱ)当
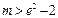 时,不等式f (x)<m恒成立.(Ⅲ)a的取值范围是
时,不等式f (x)<m恒成立.(Ⅲ)a的取值范围是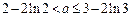
(Ⅰ)函数的定义域为(-1, +∞).…………………………………………… 1分
∵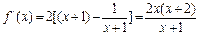 ,
,
由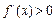 ,得x>0;由
,得x>0;由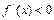 ,得
,得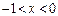 .…………………3分
.…………………3分
∴f (x)的递增区间是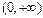 ,递减区间是(-1, 0).………………… 4分
,递减区间是(-1, 0).………………… 4分
(Ⅱ)∵由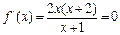 ,得x=0,x=-2(舍去)
,得x=0,x=-2(舍去)
由(Ⅰ)知f (x)在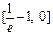 上递减,在
上递减,在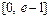 上递增.
上递增.
高三数学(理科)答案第3页(共6页)
又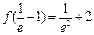 ,
,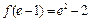 , 且
, 且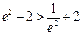 .
.
∴当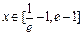 时,f (x)的最大值为
时,f (x)的最大值为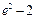 .
.
故当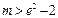 时,不等式f (x)<m恒成立.……………………………… 9分
时,不等式f (x)<m恒成立.……………………………… 9分
(Ⅲ)方程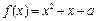 ,
, 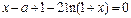 .
.
记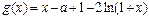 ,
,
∵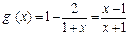 ,
,
由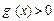 ,得x>1或x<-1(舍去). 由
,得x>1或x<-1(舍去). 由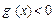 , 得
, 得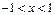 .
.
∴g(x)在[0,1]上递减, 在[1,2]上递增.
为使方程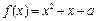 在区间[0, 2]上恰好有两个相异的实根,
在区间[0, 2]上恰好有两个相异的实根,
只须g(x)=0在[0,1]和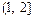 上各有一个实数根,于是有
上各有一个实数根,于是有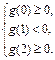
∵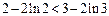 ,
,
∴实数a的取值范围是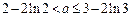 .
.
∵
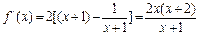 ,
, 由
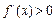 ,得x>0;由
,得x>0;由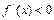 ,得
,得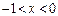 .…………………3分
.…………………3分∴f (x)的递增区间是
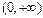 ,递减区间是(-1, 0).………………… 4分
,递减区间是(-1, 0).………………… 4分(Ⅱ)∵由
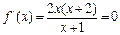 ,得x=0,x=-2(舍去)
,得x=0,x=-2(舍去)由(Ⅰ)知f (x)在
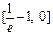 上递减,在
上递减,在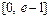 上递增.
上递增. 高三数学(理科)答案第3页(共6页)
又
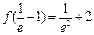 ,
,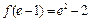 , 且
, 且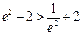 .
.∴当
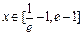 时,f (x)的最大值为
时,f (x)的最大值为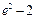 .
.故当
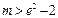 时,不等式f (x)<m恒成立.……………………………… 9分
时,不等式f (x)<m恒成立.……………………………… 9分(Ⅲ)方程
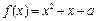 ,
, 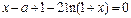 .
.记
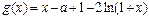 ,
,∵
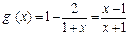 ,
, 由
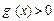 ,得x>1或x<-1(舍去). 由
,得x>1或x<-1(舍去). 由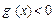 , 得
, 得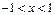 .
.∴g(x)在[0,1]上递减, 在[1,2]上递增.
为使方程
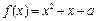 在区间[0, 2]上恰好有两个相异的实根,
在区间[0, 2]上恰好有两个相异的实根,只须g(x)=0在[0,1]和
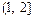 上各有一个实数根,于是有
上各有一个实数根,于是有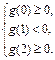
∵
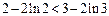 ,
, ∴实数a的取值范围是
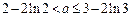 .
.
练习册系列答案
 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目
 的图象上以N(1,n)为切点的切线的倾斜角为
的图象上以N(1,n)为切点的切线的倾斜角为
 恒成立?如果存在,请求出最小的正整数k;如果不存在,请说明理由;
恒成立?如果存在,请求出最小的正整数k;如果不存在,请说明理由;
 ,函数
,函数 ,
, .
. 的单调性
的单调性 ,求证:
,求证: 有三个不同的实根.
有三个不同的实根.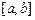 上的函数
上的函数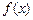 ,给出下列命题:(1)若
,给出下列命题:(1)若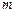 ,极小值为
,极小值为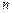 ,那么
,那么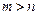 ;(3)若
;(3)若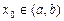 ,在
,在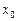 左侧附近
左侧附近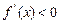 ,且
,且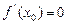 ,则
,则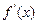 在
在 当
当 时取得极大值。当
时取得极大值。当 时取得极小值,则
时取得极小值,则 的取值范围是( )
的取值范围是( )



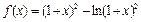 .
.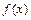 的单调区间;
的单调区间;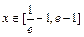 时,设函数
时,设函数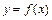 图象上任意一点处的切线的倾斜角为
图象上任意一点处的切线的倾斜角为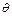 ,求
,求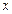 的方程
的方程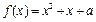 在区间[0,2]上恰好有两个相异的实根,求实数
在区间[0,2]上恰好有两个相异的实根,求实数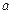 的取值范围。
的取值范围。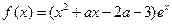 ,
,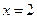 是函数
是函数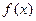 的一个极值点,求实数
的一个极值点,求实数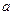 的值;
的值;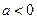 ,当
,当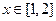 时,函数
时,函数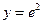 上方,求实数
上方,求实数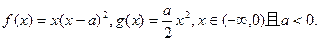
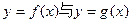 的图象的交点A的坐标;
的图象的交点A的坐标;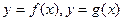 的图象在交点A处的切线分别为
的图象在交点A处的切线分别为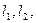 是否存在这样的实数a,使得
是否存在这样的实数a,使得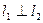 ?若存在,请求出a的值和相应的点A坐标;若不存在,请说明理由。
?若存在,请求出a的值和相应的点A坐标;若不存在,请说明理由。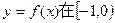 上最小值为F(a),求
上最小值为F(a),求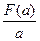 的最小值。
的最小值。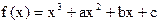 ,曲线
,曲线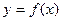 在点x=1处的切线l不过第四象限且斜率为3,又坐标原点到切线l的距离为
在点x=1处的切线l不过第四象限且斜率为3,又坐标原点到切线l的距离为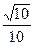 ,若
,若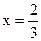 时,
时,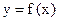 有极值.
有极值.