题目内容
【题目】如图,三棱柱![]() 所有的棱长均为1,
所有的棱长均为1,![]() C.
C.
![]() 1
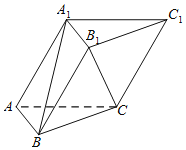
1![]() 求证:
求证:![]() ;
;
![]() 2
2![]() 若
若![]() ,求直线
,求直线![]() 和平面
和平面![]() 所成角的余弦值.
所成角的余弦值.
【答案】(1)见解析;(2)![]()
【解析】
![]() Ⅰ
Ⅰ![]() 取
取![]() 中点
中点![]() ,连接
,连接![]() ,则
,则![]() ,连接
,连接![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() ,则
,则![]() ,推导出
,推导出![]() ,从而
,从而![]() 面
面![]() ,由此能证明
,由此能证明![]() .
.
![]() Ⅱ
Ⅱ![]() 由
由![]() ,得直线
,得直线![]() 和平面
和平面![]() 所成的角等于直线
所成的角等于直线![]() 和平面
和平面![]() 所成的角,推导出
所成的角,推导出![]() ,从而
,从而![]() 面
面![]() ,进而面
,进而面![]() 面
面![]() ,推导出
,推导出![]() 为直线
为直线![]() 和平面
和平面![]() 所成的角,由此能求出直线
所成的角,由此能求出直线![]() 和平面
和平面![]() 所成的角的余弦值.
所成的角的余弦值.
![]() 1
1![]() 取AC中点O,连接
取AC中点O,连接![]() ,BO,
,BO,![]() ,
,
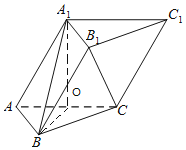
连接![]() 交
交![]() 于点M,连接OM,则
于点M,连接OM,则![]() ,
,
![]() ,
,![]() ,
,![]() ,
,
又![]() 面
面![]() ,
,![]() 面
面![]() ,
,
![]() 面
面![]() ,
,
![]() .
.
解:![]() 2
2![]() ,
,![]() 直线
直线![]() 和平面
和平面![]() 所成的角等于
所成的角等于
直线AC和平面![]() 所成的角
所成的角![]()
![]() 三棱柱
三棱柱![]() 所有的棱长均为1,
所有的棱长均为1,![]() ,
,
![]() ,
,![]() ,
,![]() 面
面![]() ,
,
![]() 面
面![]() 面
面![]()
![]() 面
面![]() 面
面![]() ,
,![]() 在平面
在平面![]() 的射影为
的射影为![]() ,
,
![]() 为直线AC和平面
为直线AC和平面![]() 所成的角
所成的角![]()
![]() ,
,
![]() ,
,![]() ,
,![]() 在
在![]() 中,
中,![]() .
.
![]() 直线AC和平面
直线AC和平面![]() 所成角的余弦值为
所成角的余弦值为![]() .
.
即直线![]() 和平面
和平面![]() 所成的角的余弦值为
所成的角的余弦值为![]()

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目