题目内容
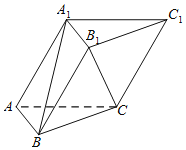
【题目】将圆的六个等分点分成相同的两组，它们每组三个点构成的两个正三角形除去内部的六条线段后可以形成一个正六角星．如图所示的正六角星的中心为点O，其中x，y分别为点O到两个顶点的向量．若将点O到正六角星12个顶点的向量都写成ax+by的形式，则a+b的最大值为 ． 
【答案】5
【解析】解：欲求a+b的最大值﹐只需考虑右图中6个顶点的向量即可，讨论如下﹔（1）∵ 
═ 
﹐∴（a，b）=（1，0）；（2）∵ 
，所以（a，b）=（3，1）；（3）∵ 
，所以（a，b）=（2，1）；（4）∵ 
，所以（a，b）=（3，2）；（5）∵ 
，所以（a，b）=（1，1）；（6）∵ 
，所以（a，b）=（0，1）； 因此﹐a+b的最大值为3+2=5﹒
所以答案是：5﹒
【考点精析】认真审题，首先需要了解平面向量的基本定理及其意义(如果
、
是同一平面内的两个不共线向量，那么对于这一平面内的任意向量
，有且只有一对实数
、
，使
)．
口算心算速算应用题系列答案
同步拓展阅读系列答案
【题目】据《中国新闻网》10月21日报道，全国很多省市将英语考试作为高考改革的重点，一时间“英语考试该如何改”引起广泛关注．为了解某地区学生和包括老师、家长在内的社会人士对高考英语改革的看法，某媒体在该地区选择了3600人调查，就是否“取消英语听力”的问题，调查统计的结果如下表：
态度 | 应该取消 | 应该保留 | 无所谓 |
在校学生 | 2100人 | 120人 | y人 |
社会人士 | 600人 | x人 | z人 |
已知在全体样本中随机抽取1人，抽到持“应该保留”态度的人的概率为0.05．
（Ⅰ）现用分层抽样的方法在所有参与调查的人中抽取360人进行问卷访谈，问应在持“无所谓”态度的人中抽取多少人？
（Ⅱ）在持“应该保留”态度的人中，用分层抽样的方法抽取6人平均分成两组进行深入交流，求第一组中在校学生人数ξ的分布列和数学期望．
