题目内容
【题目】已知数列![]() 是公比为
是公比为![]() 的等比数列,且
的等比数列,且![]() 是
是![]() 与
与![]() 的等比中项,其前
的等比中项,其前![]() 项和为
项和为![]() ;数列
;数列![]() 是等差数列,
是等差数列, ![]() ,其前
,其前![]() 项和
项和![]() 满足
满足![]() (
(![]() 为常数,且
为常数,且![]() ).
).
(1)求数列![]() 的通项公式及
的通项公式及![]() 的值;
的值;
(2)求![]() .
.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】试题分析:(1)根据1-a2是a1与1+a3的等比中项,建立关于a1的方程,解出![]() ,从而得出数列{an}的通项公式.再由Tn=nλbn+1分别取n=1、2,建立关于{bn}的公差d与λ的方程组,解之即可得到实数λ的值;(2)由等差数列的通项与求和公式算出{bn}的前n项和Tn=4n2+4n,
,从而得出数列{an}的通项公式.再由Tn=nλbn+1分别取n=1、2,建立关于{bn}的公差d与λ的方程组,解之即可得到实数λ的值;(2)由等差数列的通项与求和公式算出{bn}的前n项和Tn=4n2+4n, ![]() 利用裂项求和的方法算出
利用裂项求和的方法算出![]()
试题解析:
(1)由题意得: ![]() ,即
,即![]() ,解得
,解得![]() ,
, ![]() ;
;
设数列![]() 的公差为d,于是
的公差为d,于是![]() ,即
,即 ,即
,即![]() , 解得
, 解得 或
或![]() (舍去),
(舍去),![]() .
.
(2)由(1)知数列![]() 的首项b1=8,公差d=8,
的首项b1=8,公差d=8,
∴{bn}的前n项和Tn前![]() 项和为
项和为![]() ,
,
![]()
![]() ,
,
∴![]()
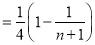

练习册系列答案
 高中必刷题系列答案
高中必刷题系列答案
相关题目

