题目内容
【题目】已知等差数列{an}的前n项和为Sn , S3=15,a3和a5的等差中项为9
(1)求an及Sn
(2)令bn= ![]() (n∈N*),求数列{bn}的前n项和Tn .
(n∈N*),求数列{bn}的前n项和Tn .
【答案】
(1)解:∵数列{an}为等差数列,所以设其首项为a1,公差为d,
∵S3=3a3,a3+a5=18,
![]() ,解得a1=3,d=2,
,解得a1=3,d=2,
∴an=a1+(n﹣1)d=2n+1,
an=2n+1,
![]() =n2+2n
=n2+2n
(2)解:由(1)知an=2n+1,
∴bn= ![]() =
= ![]() =(
=( ![]() ﹣
﹣ ![]() ),(n∈N*),
),(n∈N*),
数列{bn}的前n项和Tn,Tn=b1+b2+b3+…+bn,
=(1﹣ ![]() )+(
)+( ![]() ﹣
﹣ ![]() )+(
)+( ![]() ﹣
﹣ ![]() )+…+(
)+…+( ![]() ﹣
﹣ ![]() ),
),
=1﹣ ![]() ,
,
= ![]() .
.
【解析】(1)根据S3=15,a3和a5的等差中项为9,列方程组解得:a1=3,d=2,写出通项公式an和前n项和Sn公式;(2)由bn= ![]() =(
=( ![]() ﹣
﹣ ![]() ),采用裂项法求数列的前n项和Tn .
),采用裂项法求数列的前n项和Tn .
【考点精析】解答此题的关键在于理解等差数列的通项公式(及其变式)的相关知识,掌握通项公式:![]() 或
或![]() ,以及对数列的前n项和的理解,了解数列{an}的前n项和sn与通项an的关系
,以及对数列的前n项和的理解,了解数列{an}的前n项和sn与通项an的关系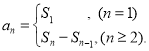 .
.

练习册系列答案
 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目