题目内容
【题目】△ABC的三个内角A、B、C的对边分别是a,b,c,给出下列命题: ①若sinBcosC>﹣cosBsinC,则△ABC一定是钝角三角形;
②若sin2A+sin2B=sin2C,则△ABC一定是直角三角形;
③若bcosA=acosB,则△ABC为等腰三角形;
④在△ABC中,若A>B,则sinA>sinB;
其中正确命题的序号是 . (注:把你认为正确的命题的序号都填上)
【答案】②③④
【解析】解:①若sinBcosC>﹣cosBsinCsinBcosC+cosBsinC=sin(B+C)>00<B+C<π,所以①不一定成立; ②∵sinA= ![]() ,sinB=
,sinB= ![]() ,sinC=
,sinC= ![]() ,∴
,∴ ![]() +
+ ![]() =
= ![]() ,即a2+b2=c2 , ∴△ABC是直角三角形,②成立,
,即a2+b2=c2 , ∴△ABC是直角三角形,②成立,
③若bcosA=acosB2rsinBcosA=2rsinAcosBsin(B﹣A)=0A=B即③成立.
④在△ABC中,若A>Ba>b2rsinA>2rsinBsinA>sinB即④成立;
故正确命题的是②③④.
所以答案是:②③④.
【考点精析】根据题目的已知条件,利用命题的真假判断与应用的相关知识可以得到问题的答案,需要掌握两个命题互为逆否命题,它们有相同的真假性;两个命题为互逆命题或互否命题,它们的真假性没有关系.

练习册系列答案
相关题目
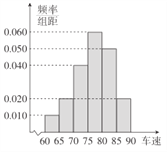
【题目】某公司2016年前三个月的利润(单位:百万元)如下:
月份 | 1 | 2 | 3 |
利润 | 2 | 3.9 | 5.5 |
(1)求利润![]() 关于月份
关于月份![]() 的线性回归方程;
的线性回归方程;
(2)试用(1)中求得的回归方程预测4月和5月的利润;
(3)试用(1)中求得的回归方程预测该公司2016年从几月份开始利润超过1000万?
相关公式: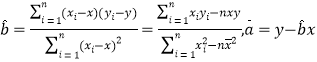 .
.