题目内容
已知定义在[0,+∞)上的函数f(x),当x∈[0,1]时,f(x)=2-4|x-
|;当x>1时,f(x)=af(x-1),a∈R,a为常数.下列有关函数f(x)的描述:
①当a=2时,f(
)=4;
②当|a|<1,函数f(x)的值域为[-2,2];
③当a>0时,不等式f(x)≤2ax-
在区间[0,+∞)上恒成立;
④当-1<a<0时,函数f(x)的图象与直线y=2an-1(n∈N*)在[0,n]内的交点个数为n-
.
其中描述正确的个数有( )
| 1 |
| 2 |
①当a=2时,f(
| 3 |
| 2 |
②当|a|<1,函数f(x)的值域为[-2,2];
③当a>0时,不等式f(x)≤2ax-
| 1 |
| 2 |
④当-1<a<0时,函数f(x)的图象与直线y=2an-1(n∈N*)在[0,n]内的交点个数为n-
| 1+(-1)n |
| 2 |
其中描述正确的个数有( )
| A、4 | B、3 | C、2 | D、1 |
考点:命题的真假判断与应用,分段函数的应用
专题:函数的性质及应用
分析:对于描述①,将a=2及x=
代入f(x)=af(x-1)中,再利用x∈[0,1]时的函数关系式,可得f(
)的值;
对于描述②,分“-1<a<0”,“a=0”,“0<a<1”三种情况,观察f(x)图象的最高点与最低点,可得函数的值域;
对于描述③,利用赋值法,可尝试给定a一个较大的值代入,即可否定;
对于描述④,先考虑n=1,2,3,4时的情形,由此发现规律,再用数学归纳法证明.
| 3 |
| 2 |
| 3 |
| 2 |
对于描述②,分“-1<a<0”,“a=0”,“0<a<1”三种情况,观察f(x)图象的最高点与最低点,可得函数的值域;
对于描述③,利用赋值法,可尝试给定a一个较大的值代入,即可否定;
对于描述④,先考虑n=1,2,3,4时的情形,由此发现规律,再用数学归纳法证明.
解答:解:由题意知,f(x)=
.
在描述①中,由x>1,将a=2及x=
代入f(x)=af(x-1)中,
得f(
)=2f(
-1)=2f(
)=2(2-4|
-
|)=4,可知描述①正确.
在描述②中,
(1)若0<a<1,当0≤x≤1时,f(x)=
,其图象是一条折线段,
当x>1时,则f(x)的图象向右依次平移一个单位长度,
且每条折线段的转折点到x轴的距离是上一条折线段的转折点到x轴距离的a倍,
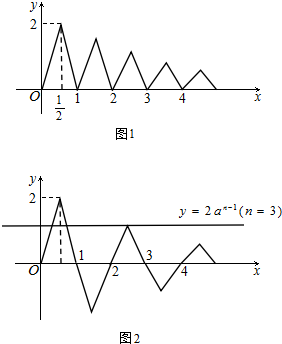
由f(
)=2知,0≤f(x)≤2.其图象如图1所示.
(2)若a=0,则f(x)=
,此时亦有0≤f(x)≤2.
(3)若-1<a<0,则f(x)的图象向右依次平移一个单位长度,每条折线段在x轴上下交替出现,
且从第二段起,每条折线段的转折点到x轴的距离是上一条折线段的转折点到x轴距离的|a|倍,
此时,-2<f(x)≤2.其图象如图2所示.
综合(1),(2),(3)知,f(x)的值域为(-2,2],所以描述②错.
在描述③中,取a=44,x=
,则f(
)=2-4|
-
|=1,
而2ax-
=2×(44)
-
=
<1,故描述③错.
在描述④中,由图2知,
当n=1时,f(x)的图象与直线y=2a1-1即y=2在[0,1]内的交点个数为1,即1-
;
当n=2时,f(x)的图象与直线y=2a2-1即y=2a在[0,2]内的交点个数为1,即2-
;
当n=3时,f(x)的图象与直线y=2a3-1即y=2a2在[0,3]内的交点个数为3,即3-
;
当n=4时,f(x)的图象与直线y=2a4-1即y=2a3在[0,4]内的交点个数为3,即4-
;
…
由此猜想:当-1<a<0时,函数f(x)的图象与直线y=2an-1(n∈N*)在[0,n]内的交点个数为n-
.
现用数学归纳法证明之.
(1)由上可知,当n=1时,猜想成立.
(2)假设n=k时,猜想成立,即函数f(x)的图象与直线y=2ak-1(k∈N*)在[0,k]内的交点个数为k-
.
则当n=k+1时,如图2所示,若k为奇数,则交点个数与n=k时情形相同;
若k为偶数,则交点个数在n=k时的基础上增加2个,
所以当n=k+1时的交点个数在n=k时的基础上增加了1+(-1)k个,
从而交点个数为k-
+1+(-1)k=k+1-
,得(k+1)-
,
即当n=k+1时,猜想也成立.
综合(1),(2)知,猜想成立,所以描述④正确.
故①④正确,选C.
|

在描述①中,由x>1,将a=2及x=
| 3 |
| 2 |
得f(
| 3 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
在描述②中,
(1)若0<a<1,当0≤x≤1时,f(x)=
|
当x>1时,则f(x)的图象向右依次平移一个单位长度,
且每条折线段的转折点到x轴的距离是上一条折线段的转折点到x轴距离的a倍,
由f(
| 1 |
| 2 |
(2)若a=0,则f(x)=
|
(3)若-1<a<0,则f(x)的图象向右依次平移一个单位长度,每条折线段在x轴上下交替出现,
且从第二段起,每条折线段的转折点到x轴的距离是上一条折线段的转折点到x轴距离的|a|倍,
此时,-2<f(x)≤2.其图象如图2所示.
综合(1),(2),(3)知,f(x)的值域为(-2,2],所以描述②错.
在描述③中,取a=44,x=
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 2 |
而2ax-
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
在描述④中,由图2知,
当n=1时,f(x)的图象与直线y=2a1-1即y=2在[0,1]内的交点个数为1,即1-
| 1+(-1)1 |
| 2 |
当n=2时,f(x)的图象与直线y=2a2-1即y=2a在[0,2]内的交点个数为1,即2-
| 1+(-1)2 |
| 2 |
当n=3时,f(x)的图象与直线y=2a3-1即y=2a2在[0,3]内的交点个数为3,即3-
| 1+(-1)3 |
| 2 |
当n=4时,f(x)的图象与直线y=2a4-1即y=2a3在[0,4]内的交点个数为3,即4-
| 1+(-1)4 |
| 2 |
…
由此猜想:当-1<a<0时,函数f(x)的图象与直线y=2an-1(n∈N*)在[0,n]内的交点个数为n-
| 1+(-1)n |
| 2 |
现用数学归纳法证明之.
(1)由上可知,当n=1时,猜想成立.
(2)假设n=k时,猜想成立,即函数f(x)的图象与直线y=2ak-1(k∈N*)在[0,k]内的交点个数为k-
| 1+(-1)k |
| 2 |
则当n=k+1时,如图2所示,若k为奇数,则交点个数与n=k时情形相同;
若k为偶数,则交点个数在n=k时的基础上增加2个,
所以当n=k+1时的交点个数在n=k时的基础上增加了1+(-1)k个,
从而交点个数为k-
| 1+(-1)k |
| 2 |
| 1-(-1)k |
| 2 |
| 1+(-1)k+1 |
| 2 |
即当n=k+1时,猜想也成立.
综合(1),(2)知,猜想成立,所以描述④正确.
故①④正确,选C.
点评:1.本题以绝对值函数为载体,考查了分段函数的解析式,值域及图象,尤其是图象间的平移与伸缩变换,考查了数形结合、分类讨论思想的运用与归纳推理能力.对分段函数问题,一般采取分段处理的方法,但“分段不分家”,应具备整体思想,必要时可画出图形结合分析.值得注意的是,在临界点处的情形应该谨慎对待.
2.要说明一个命题为真,必须有严密的逻辑推理;要说明一个命题为假,只需举一反例即可.
2.要说明一个命题为真,必须有严密的逻辑推理;要说明一个命题为假,只需举一反例即可.

练习册系列答案
 新编小学单元自测题系列答案
新编小学单元自测题系列答案
相关题目
在△ABC中,A-B=
,sinC=
,AB=
,则AC=( )
| π |
| 2 |
| 1 |
| 3 |
| 3 |
A、
| ||||
B、
| ||||
| C、3 | ||||
D、3
|
已知命题p:a=1是?x>0,x+
≥2的充要条件:命题q:?x∈R,x2-x+1<0.则下列结论中正确的是( )
| a |
| x |
| A、p∧q为真命题 |
| B、p∧¬q为真命题 |
| C、¬p∧q为真命题 |
| D、¬p∧¬q为真命题 |
定义“正对数”:ln+x=
,现有四个命题:
①若a>0,b>0,则ln+(ab)=bln+a
②若a>0,b>0,则ln+(ab)=ln+a+ln+b
③若a>0,b>0,则ln+(
)≥ln+a-ln+b
④若a>0,b>0,则ln+(a+b)≤ln+a+ln+b+ln2
其中正确的命题有( )
|
①若a>0,b>0,则ln+(ab)=bln+a
②若a>0,b>0,则ln+(ab)=ln+a+ln+b
③若a>0,b>0,则ln+(
| a |
| b |
④若a>0,b>0,则ln+(a+b)≤ln+a+ln+b+ln2
其中正确的命题有( )
| A、①③④ | B、①②③ |
| C、①②④ | D、②③④ |
若p:φ=
+kπ,k∈Z,q:f(x)=sin(ωx+φ)(ω≠0)是偶函数,则p是q的( )
| π |
| 2 |
| A、充要条件 |
| B、充分不必要条件 |
| C、必要不充分条件 |
| D、既不充分也不必要条件 |
设平面α与平面β相交于直线l,直线a?α,直线b?β,b∥l,则“a∥β”是“a∥b”的( )
| A、充分而不必要条件 | B、必要而不充分条件 | C、充要条件 | D、既不充分又不必要条件 |
已知曲线C1:
+y2=1和C2:x2-y2=1的焦点分别为F1、F2,点M是C1和C2的一个交点,则△MF1F2的形状是( )
| x2 |
| 3 |
| A、锐角三角形 | B、直角三角形 |
| C、钝角三角形 | D、不能确定 |