题目内容
①两直线m,n与平面α所成的角相等的充要条件是m∥n;
②设a,b是两条直线,α,β是两个平面,则a⊥b的一个充分条件是a⊥α,b⊥β,α∥β;
③若p:对?x∈R,sinx≤1,则﹁p:对?x∈R,sinx>1;
④设有四个函数y=x-1,y=x
,y=x
,y=x3,其中在定义域上是增函数的有3个;
⑤设方程2lnx=7-2x的解x0,则关于x的不等式x-2<x0的最大整数解为x=4.
其中正确的命题的个数( )
②设a,b是两条直线,α,β是两个平面,则a⊥b的一个充分条件是a⊥α,b⊥β,α∥β;
③若p:对?x∈R,sinx≤1,则﹁p:对?x∈R,sinx>1;
④设有四个函数y=x-1,y=x
| 1 |
| 2 |
| 1 |
| 3 |
⑤设方程2lnx=7-2x的解x0,则关于x的不等式x-2<x0的最大整数解为x=4.
其中正确的命题的个数( )
| A、1 | B、2 | C、3 | D、0 |
考点:命题的真假判断与应用
专题:综合题,简易逻辑
分析:①两直线m,n与平面α所成的角相等,则m∥n不一定成立,反之成立;
②若a⊥α,α∥β,则a⊥β,又b⊥β,所以a∥b;
③根据全称命题的否定是特称命题可知分别对量词及命题的结论进行否定即可;
④y=x
,y=x
,y=x3,在定义域上是增函数;
⑤由方程2Inx=7-2x的解为x0,我们易得函数y=2Inx-7+2x的零点为x0,根据函数零点的判定定理,我们可得x0∈(2,3),根据不等式的性质我们易求出等式x-2<x0的最大整数解.
②若a⊥α,α∥β,则a⊥β,又b⊥β,所以a∥b;
③根据全称命题的否定是特称命题可知分别对量词及命题的结论进行否定即可;
④y=x
| 1 |
| 2 |
| 1 |
| 3 |
⑤由方程2Inx=7-2x的解为x0,我们易得函数y=2Inx-7+2x的零点为x0,根据函数零点的判定定理,我们可得x0∈(2,3),根据不等式的性质我们易求出等式x-2<x0的最大整数解.
解答:解:①两直线m,n与平面α所成的角相等,则m∥n不一定成立,反之成立,故①不正确;
②若a⊥α,α∥β,则a⊥β,又b⊥β,所以a∥b,故②不正确;
③根据全称命题的否定是特称命题可知,p:?x∈R,sinx≤1的否定为?x∈R,使得sinx>1,故③不正确;
④y=x
,y=x
,y=x3,在定义域上是增函数,故正确;
⑤因为方程2Inx=7-2x的解为x0,所以x0为函数函数y=2Inx-7+2x的零点,由函数y=2Inx在其定义域为单调递增,y=7-2x在其定义域为单调递减,故函数函数y=2Inx-7+2x至多有一个零点,
由f(2)=2In2-7+2×2<0f(3)=2In3-7+2×3>0知,x0∈(2,3),
则x-2<x0可化为x<x0+2,则满足条件的最大整数解为4,故正确.
故选:B.
②若a⊥α,α∥β,则a⊥β,又b⊥β,所以a∥b,故②不正确;
③根据全称命题的否定是特称命题可知,p:?x∈R,sinx≤1的否定为?x∈R,使得sinx>1,故③不正确;
④y=x
| 1 |
| 2 |
| 1 |
| 3 |
⑤因为方程2Inx=7-2x的解为x0,所以x0为函数函数y=2Inx-7+2x的零点,由函数y=2Inx在其定义域为单调递增,y=7-2x在其定义域为单调递减,故函数函数y=2Inx-7+2x至多有一个零点,
由f(2)=2In2-7+2×2<0f(3)=2In3-7+2×3>0知,x0∈(2,3),
则x-2<x0可化为x<x0+2,则满足条件的最大整数解为4,故正确.
故选:B.
点评:本题考查命题的真假判断与应用,考查学生分析解决问题的能力,知识综合性强.

练习册系列答案
相关题目
如果sin2θ+2sinθ>cos2θ+2cosθ,且θ∈(0,2π),那么角θ的取值范围是( )
A、(0,
| ||||
B、(
| ||||
C、(
| ||||
D、(
|
原命题为“若
<an,n∈N+,则{an}为递减数列”,关于其逆命题,否命题,逆否命题真假性的判断依次如下,正确的是( )
| an+an+1 |
| 2 |
| A、真、真、真 |
| B、假、假、真 |
| C、真、真、假 |
| D、假、假、假 |
下列有关命题的说法正确的是( )
| A、命题“x2=1,则x=1”的否命题为“若x2=1,则x≠1” | B、命题“?x∈R,x2+x-1<0”的否定是“?x∈R,x2+x-1>0” | C、若“p∨q”为真命题,则p,q至少有一个为真命题 | D、命题“若x=y,则sinx=siny”的逆命题为假命题 |
不等式x+
≥2成立的一个必要不充分条件是( )
| 1 |
| x |
| A、(0,+∞) |
| B、(0,1) |
| C、(-1,+∞) |
| D、(1,+∞) |
已知回归直线的斜率的估计值是1.2,样本点的中心为(4,5),则回归直线方程是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
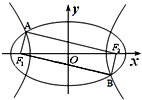 如图,F1、F2是椭圆C1与双曲线C2:
如图,F1、F2是椭圆C1与双曲线C2: