题目内容
已知曲线C1:
+y2=1和C2:x2-y2=1的焦点分别为F1、F2,点M是C1和C2的一个交点,则△MF1F2的形状是( )
| x2 |
| 3 |
| A、锐角三角形 | B、直角三角形 |
| C、钝角三角形 | D、不能确定 |
考点:椭圆的简单性质,双曲线的简单性质
专题:圆锥曲线的定义、性质与方程
分析:由已知条件分别求出F1(-
,0),F2(
,0),不妨设M(
,
),分别求出△MF1F2的三条边,用余弦定理能判断△MF1F2的形状.
| 2 |
| 2 |
| ||
| 2 |
| ||
| 2 |
解答:解:∵曲线C1:
+y2=1和C2:x2-y2=1的焦点分别为F1、F2,
∴F1(-
,0),F2(
,0),
∵点M是C1和C2的一个交点,
联立
,得x2=
,y2=
,
∴不妨设M(
,
),
则|MF1|=
=
=1+
,
|MF2|=
=
-1,
|F1F2|=2
,
∵△MF1F2的三条边中|F1F2|最长,∴∠F1MF2最大,
∴cos∠F1MF2=
=0,
∴△MF1F2是直角三角形.
故选:B.
| x2 |
| 3 |
∴F1(-
| 2 |
| 2 |
∵点M是C1和C2的一个交点,
联立
|
| 3 |
| 2 |
| 1 |
| 2 |
∴不妨设M(
| ||
| 2 |
| ||
| 2 |
则|MF1|=
(
|
4+2
|
| 3 |
|MF2|=
(
|
| 3 |
|F1F2|=2
| 2 |
∵△MF1F2的三条边中|F1F2|最长,∴∠F1MF2最大,
∴cos∠F1MF2=
(1+
| ||||||
2(1+
|
∴△MF1F2是直角三角形.
故选:B.
点评:本题考查三角形的形状的判断,是中档题,解题时要认真审题,注意余弦定理的合理运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知变量x,y满足约束条件
,则z=x2+y2+2的最大值( )
|
| A、15 | B、17 | C、18 | D、19 |
已知直线l⊥平面α,且l不在平面β内,则“α⊥β”是“l∥β”的( )
| A、充分不必要条件 | B、必要不充分条件 | C、充要条件 | D、既不是充分条件,也不是必要条件 |
过双曲线C:
-
=1的右顶点做x轴的垂线,与C的一条渐近线相交于点A,若以C的右焦点为圆心、半径为4的圆经过A,O两点(O为坐标原点),则双曲线C的方程为( )
| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
设抛物线C的方程y2=4x,O为坐标原点,P为抛物线的准线与其对称轴的交点,过焦点F且垂直于x轴的直线交抛物线于M,N两点,若直线PM与ON相交于点Q,则cos∠MQN=( )
A、
| ||||
B、-
| ||||
C、
| ||||
D、-
|
已知f(x)=
x4-
x3+2x2+a在x=x1处取得极值2,则
dt=( )
| 1 |
| 4 |
| 4 |
| 3 |
| ∫ | 1 0 |
| a2-t2 |
A、π+
| ||||||||||||
| B、π | ||||||||||||
C、
| ||||||||||||
D、
|
i为虚数单位,复数z=1+i的模为( )
| A、1 | ||
B、
| ||
C、
| ||
| D、2 |
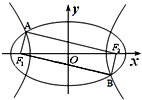 如图,F1、F2是椭圆C1与双曲线C2:
如图,F1、F2是椭圆C1与双曲线C2: