题目内容
13．已知定义在R上的函数f（x）是奇函数，对x∈R都有f（2+x）=-f（2-x），则f（2016）=（ ）| A． | 2 | B． | -2 | C． | 4 | D． | 0 |
分析 利用函数的奇偶性以及抽象函数求出函数的周期，然后求解函数值即可．
解答 解：∵f（x）在R上是奇函数且f（2+x）=-f（2-x），可得f（0）=0．
∴f（2+x）=-f（2-x）=f（x-2），∴f（x）=f（x+4），故函数f（x）是以4为周期的周期函数，
∴f（2016）=f（0）=0．
故选：D．
点评 本题考查抽象函数的应用，函数的正确以及函数的奇偶性的应用，考查计算能力．
练习册系列答案
相关题目
4．
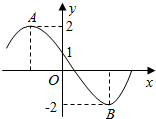函数f（x）=2sin（ωx+φ）的部分图象如图所示，其中A，B两点之间的距离为5，那么下列说法正确的是（ ）
函数f（x）=2sin（ωx+φ）的部分图象如图所示，其中A，B两点之间的距离为5，那么下列说法正确的是（ ）| A． | 函数f（x）的最小正周期为8 | |
| B． | f（3）=-$\frac{1}{2}$ | |
| C． | x=$\frac{3}{2}$是函数f（x）的一条对称轴 | |
| D． | 函数f（x）向右平移一个单位长度后所得的函数为偶函数 |