题目内容
下列函数中，x=0是极值点的函数是（ ）
| A．y=-x3 | B．y=cos2x | C．y=tanx-x | D．y=
|
①∵y=-x3，∴y′=-2x2≤0，∴函数在x∈R上是减函数，∴x=0不是函数的极值点；
②∵y=cos2x，∴y′=-2cosxsinx=-sin2x；当-
＜x＜0时，y′＞0，函数是增函数，当0＜x＜
时，y′＜0，函数是减函数；，∴x=0是函数的极值点；
③∵y=tanx-x，∴y′=
-1≥0，∴函数在它的定义域上是增函数，∴x=0不是函数的极值点；
④∵y=
，y′=-
＜0，∴函数在它的定义域上是减函数，∴x=0不是函数的极值点；
故选：B．
②∵y=cos2x，∴y′=-2cosxsinx=-sin2x；当-
| π |
| 2 |
| π |
| 2 |
③∵y=tanx-x，∴y′=
| 1 |
| cos2x |
④∵y=
| 1 |
| x |
| 1 |
| x2 |
故选：B．
练习册系列答案
黄冈冠军课课练系列答案
相关题目
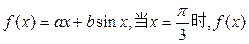取得极小值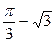
.
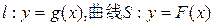. 若直线l与曲线S同时满足下列两个条件：
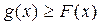. 则称直线l为曲线S的“上夹线”.
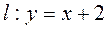是曲线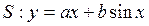
的“上夹线”.
，
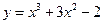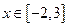的值域。