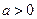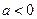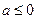题目内容
已知函数f(x)=12x-x3,求曲线y=f(x)斜率为9的切线的方程.
由题意得,f′(x)=12-3x2=9,解得x=1或x=-1,
当x=1时,切点为(1,11),故切线方程为y-11=9(x-1),即y=9x+2
当x=-1时,切点为(-1,-11),故切线方程为y+11=9(x+1),即y=9x-2
当x=1时,切点为(1,11),故切线方程为y-11=9(x-1),即y=9x+2
当x=-1时,切点为(-1,-11),故切线方程为y+11=9(x+1),即y=9x-2

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目

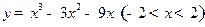 有( )
有( )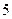 ,极小值
,极小值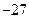 ,B 极大值
,B 极大值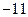 ,C 极大值
,C 极大值 有极值的充要条件是( )
有极值的充要条件是( )