题目内容
已知函数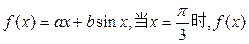 取得极小值
取得极小值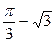 .
.
(Ⅰ)求a,b的值;
(Ⅱ)设直线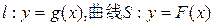 . 若直线l与曲线S同时满足下列两个条件:
. 若直线l与曲线S同时满足下列两个条件:
(1)直线l与曲线S相切且至少有两个切点;
(2)对任意x∈R都有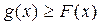 . 则称直线l为曲线S的“上夹线”.
. 则称直线l为曲线S的“上夹线”.
试证明:直线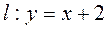 是曲线
是曲线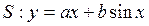 的“上夹线”.
的“上夹线”.
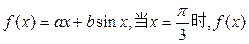 取得极小值
取得极小值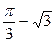 .
.(Ⅰ)求a,b的值;
(Ⅱ)设直线
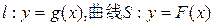 . 若直线l与曲线S同时满足下列两个条件:
. 若直线l与曲线S同时满足下列两个条件:(1)直线l与曲线S相切且至少有两个切点;
(2)对任意x∈R都有
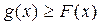 . 则称直线l为曲线S的“上夹线”.
. 则称直线l为曲线S的“上夹线”.试证明:直线
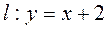 是曲线
是曲线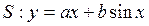 的“上夹线”.
的“上夹线”.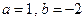 ,
,解:(I)因为 ,所以
,所以
 ,
,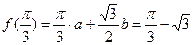
解得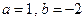 ,
,
此时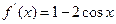 ,当
,当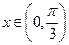 时
时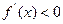 ,当
,当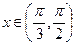 时
时 ,
,
所以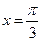 时
时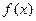 取极小值,所以
取极小值,所以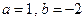 符合题目条件;
符合题目条件;
(II)由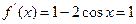 得
得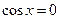 ,
,
当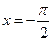 时,
时,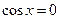 ,此时
,此时 ,
,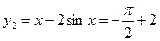 ,
,
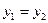 ,所以
,所以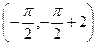 是直线
是直线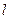 与曲线
与曲线 的一个切点;
的一个切点;
当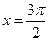 时,
时,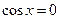 ,此时
,此时 ,
, ,
,
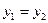 ,所以
,所以 是直线
是直线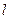 与曲线
与曲线 的一个切点;
的一个切点;
所以直线l与曲线S相切且至少有两个切点;
对任意x∈R,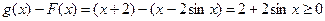 ,所以
,所以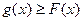
因此直线 是曲线
是曲线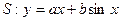 的“上夹线”.
的“上夹线”.
 ,所以
,所以
 ,
,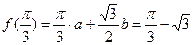
解得
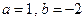 ,
,此时
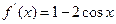 ,当
,当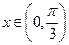 时
时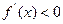 ,当
,当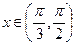 时
时 ,
, 所以
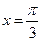 时
时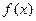 取极小值,所以
取极小值,所以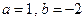 符合题目条件;
符合题目条件; (II)由
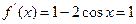 得
得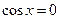 ,
,当
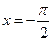 时,
时,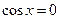 ,此时
,此时 ,
,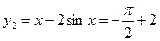 ,
,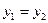 ,所以
,所以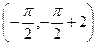 是直线
是直线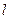 与曲线
与曲线 的一个切点;
的一个切点; 当
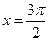 时,
时,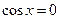 ,此时
,此时 ,
, ,
,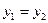 ,所以
,所以 是直线
是直线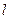 与曲线
与曲线 的一个切点;
的一个切点; 所以直线l与曲线S相切且至少有两个切点;
对任意x∈R,
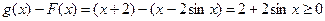 ,所以
,所以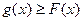
因此直线
 是曲线
是曲线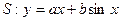 的“上夹线”.
的“上夹线”. 
练习册系列答案
相关题目
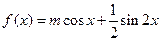 在
在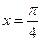 处取得极值,则
处取得极值,则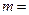 .
.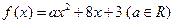 . (1)若
. (1)若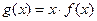 ,
, 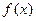 与
与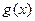 在
在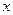 同一个值时都取极值,求
同一个值时都取极值,求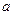 ; (2)对于给定的负数
; (2)对于给定的负数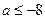 时有一个最大的正数
时有一个最大的正数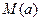 ,使得
,使得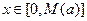 时,恒有
时,恒有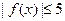 . (i)求
. (i)求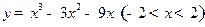 有( )
有( )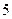 ,极小值
,极小值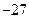 ,B 极大值
,B 极大值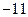 ,C 极大值
,C 极大值 有极值的充要条件是( )
有极值的充要条件是( )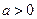

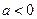
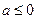
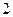 的是( )
的是( )