题目内容
若椭圆上存在一点P,使得点P到两焦点的距离之比为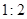 ,则此椭圆离心率的取值范围是( )
,则此椭圆离心率的取值范围是( )
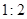 ,则此椭圆离心率的取值范围是( )
,则此椭圆离心率的取值范围是( )A.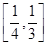 | B.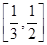 | C.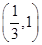 | D.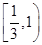 |
D
分析:设椭圆上点P到两焦点F1、F2距离比为1:2,则PF1=r,PF2=2r,可得2a=PF1+PF2=3r.再由椭圆上动点P满足|PF1-PF2|≤2c,可得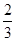 a≤6c,最后结合椭圆的离心率满足0<e<1,得到该椭圆的离心率e的取值范围.
a≤6c,最后结合椭圆的离心率满足0<e<1,得到该椭圆的离心率e的取值范围.
解答:解:设椭圆的两焦点分别为F1、F2,
∵点P到两焦点F1、F2距离比为1:2,
∴设PF1=r,则PF2=2r,可得2a=PF1+PF2=3r,r=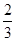 a
a
∵|PF1-PF2|=r≤2c,(当P点在F2F1延长线上时,取等号)
∴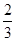 a≤2c,所以椭圆离心率e=
a≤2c,所以椭圆离心率e=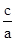 ≥
≥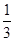
又∵椭圆的离心率满足0<e<1,
∴该椭圆的离心率e∈[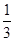 ,1)
,1)
故答案为D
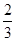 a≤6c,最后结合椭圆的离心率满足0<e<1,得到该椭圆的离心率e的取值范围.
a≤6c,最后结合椭圆的离心率满足0<e<1,得到该椭圆的离心率e的取值范围.解答:解:设椭圆的两焦点分别为F1、F2,
∵点P到两焦点F1、F2距离比为1:2,
∴设PF1=r,则PF2=2r,可得2a=PF1+PF2=3r,r=
 a
a∵|PF1-PF2|=r≤2c,(当P点在F2F1延长线上时,取等号)
∴
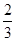 a≤2c,所以椭圆离心率e=
a≤2c,所以椭圆离心率e=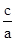 ≥
≥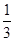
又∵椭圆的离心率满足0<e<1,
∴该椭圆的离心率e∈[
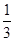 ,1)
,1)故答案为D

练习册系列答案
相关题目
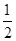 的椭圆E的一个焦点为圆C:x2+y2-4x+2=0的圆心.
的椭圆E的一个焦点为圆C:x2+y2-4x+2=0的圆心.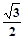 ,它与直线x+y+1=0交于P、Q两点,若OP⊥OQ,求椭圆方程。(O为原点)。
,它与直线x+y+1=0交于P、Q两点,若OP⊥OQ,求椭圆方程。(O为原点)。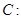
 的离心率为
的离心率为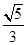 ,定点
,定点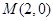 ,椭圆短轴的端点是
,椭圆短轴的端点是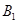 ,
,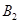 ,且
,且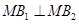 .
.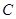 的方程;
的方程;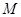 且斜率不为
且斜率不为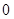 的直线交椭圆
的直线交椭圆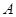 ,
,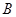 两点.试问
两点.试问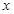 轴上是否存在定点
轴上是否存在定点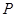 ,使
,使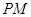 平分
平分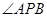 ?若存在,求出点
?若存在,求出点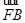 ⊥
⊥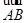 时,其离心率为
时,其离心率为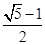 ,此类椭圆被称为“黄金椭圆”.类比“黄金椭圆”,可推算出“黄金双曲线”的离心率e等于( )
,此类椭圆被称为“黄金椭圆”.类比“黄金椭圆”,可推算出“黄金双曲线”的离心率e等于( )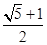
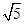 -1
-1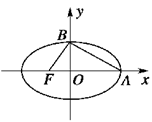
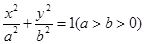 的右焦点,过原点的直线交椭圆于点A、P,PF垂直于x轴,直线AF交椭圆于点B,
的右焦点,过原点的直线交椭圆于点A、P,PF垂直于x轴,直线AF交椭圆于点B,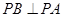 ,则该椭圆的离心率
,则该椭圆的离心率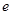 =___▲___.
=___▲___.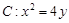 与过它的焦点F的直线
与过它的焦点F的直线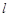 所围成封闭曲面图形的面积为
所围成封闭曲面图形的面积为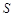 (阴影部分)。
(阴影部分)。 交于两点
交于两点 ,且
,且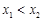 ,直线
,直线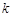 ,试用
,试用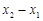 ;
;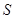 的最小值。
的最小值。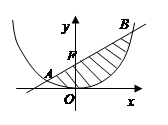
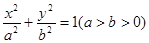 过点(0,4),(5,0).
过点(0,4),(5,0).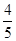 的直线被椭圆C所截线段的中点坐标
的直线被椭圆C所截线段的中点坐标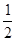 ,椭圆上一点P到两个焦点的距离之和为8,
,椭圆上一点P到两个焦点的距离之和为8,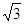 x的双曲线方程
x的双曲线方程