题目内容
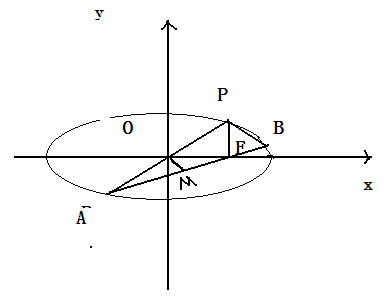
已知点F是椭圆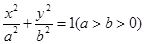 的右焦点,过原点的直线交椭圆于点A、P,PF垂直于x轴,直线AF交椭圆于点B,
的右焦点,过原点的直线交椭圆于点A、P,PF垂直于x轴,直线AF交椭圆于点B,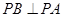 ,则该椭圆的离心率
,则该椭圆的离心率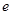 =___▲___.
=___▲___.
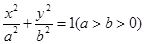 的右焦点,过原点的直线交椭圆于点A、P,PF垂直于x轴,直线AF交椭圆于点B,
的右焦点,过原点的直线交椭圆于点A、P,PF垂直于x轴,直线AF交椭圆于点B,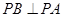 ,则该椭圆的离心率
,则该椭圆的离心率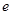 =___▲___.
=___▲___.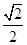
此题考查椭圆的相关性质和直线方程的相关知识,利用结论:若椭圆的方程为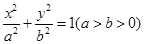 ,即焦点在
,即焦点在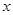 轴上,若直线
轴上,若直线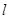 与椭圆相交,被椭圆所截得弦为
与椭圆相交,被椭圆所截得弦为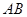 ,其中点设为
,其中点设为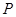 ,则该直线的斜率与该弦的中点与原点的斜率之积为常数,即
,则该直线的斜率与该弦的中点与原点的斜率之积为常数,即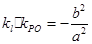 ;求解较简单;
;求解较简单;
由已知得,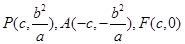 ,取
,取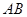 中点
中点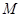 ,可知
,可知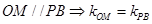 ,又因为
,又因为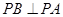 ,所以
,所以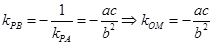 ,又因为
,又因为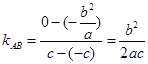 ,由
,由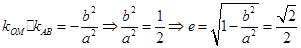 ,
,
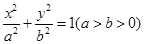 ,即焦点在
,即焦点在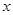 轴上,若直线
轴上,若直线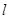 与椭圆相交,被椭圆所截得弦为
与椭圆相交,被椭圆所截得弦为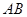 ,其中点设为
,其中点设为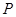 ,则该直线的斜率与该弦的中点与原点的斜率之积为常数,即
,则该直线的斜率与该弦的中点与原点的斜率之积为常数,即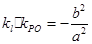 ;求解较简单;
;求解较简单;
由已知得,
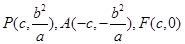 ,取
,取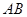 中点
中点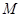 ,可知
,可知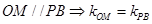 ,又因为
,又因为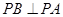 ,所以
,所以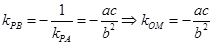 ,又因为
,又因为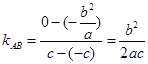 ,由
,由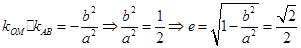 ,
,
练习册系列答案
相关题目
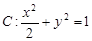 的左、右焦点分别为
的左、右焦点分别为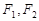 ,下顶点为
,下顶点为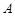 ,点
,点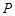 是椭圆上任一点,圆
是椭圆上任一点,圆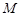 是以
是以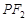 为直径的圆.
为直径的圆.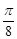 ,求
,求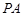 所在的直线方程;
所在的直线方程;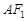 相切时,求圆
相切时,求圆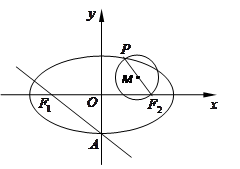
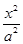 +
+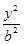 =1(a>b>0)上的点M (1,
=1(a>b>0)上的点M (1, 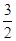 )到它的两焦点F1,F2的距离之和为4,A、B分别是它的左顶点和上顶点。
)到它的两焦点F1,F2的距离之和为4,A、B分别是它的左顶点和上顶点。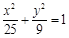 上一点P到它的一个焦点的距离等于3,那么点P到另一个焦点的距离等于 .
上一点P到它的一个焦点的距离等于3,那么点P到另一个焦点的距离等于 . 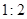 ,则此椭圆离心率的取值范围是( )
,则此椭圆离心率的取值范围是( )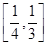
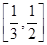
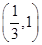
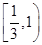
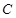 :
: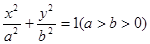 . 称圆心在原点
. 称圆心在原点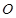 ,半径为
,半径为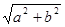 的圆是椭圆
的圆是椭圆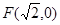 ,其短轴上的一个端点到
,其短轴上的一个端点到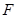 的距离为
的距离为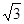 .
.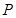 是椭圆
是椭圆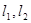 ,使得
,使得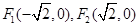 动点
动点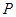 满足
满足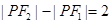 ,当点
,当点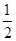 时,点
时,点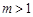 ,直线
,直线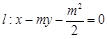 ,椭圆
,椭圆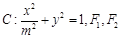 分别为椭圆
分别为椭圆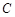 的左、右焦点.
的左、右焦点.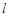 过右焦点
过右焦点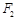 时,求直线
时,求直线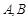 两点,
两点,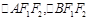 的重心分别为
的重心分别为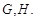 若原点
若原点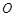 在以线段
在以线段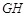 为直径的圆内,求实数
为直径的圆内,求实数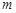 的取值范围.
的取值范围.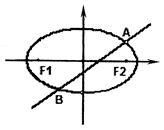
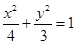 ,
,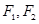 为椭圆C的两焦点,P为椭圆C上一点,连接
为椭圆C的两焦点,P为椭圆C上一点,连接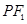 并
并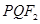 的周长_______
的周长_______