题目内容
已知椭圆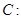
 的离心率为
的离心率为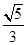 ,定点
,定点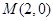 ,椭圆短轴的端点是
,椭圆短轴的端点是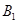 ,
,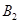 ,且
,且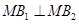 .
.
(Ⅰ)求椭圆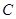 的方程;
的方程;
(Ⅱ)设过点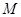 且斜率不为
且斜率不为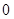 的直线交椭圆
的直线交椭圆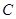 于
于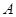 ,
,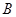 两点.试问
两点.试问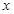 轴上是否存在定点
轴上是否存在定点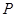 ,使
,使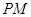 平分
平分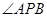 ?若存在,求出点
?若存在,求出点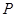 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
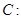
 的离心率为
的离心率为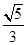 ,定点
,定点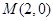 ,椭圆短轴的端点是
,椭圆短轴的端点是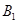 ,
,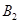 ,且
,且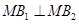 .
.(Ⅰ)求椭圆
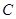 的方程;
的方程;(Ⅱ)设过点
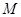 且斜率不为
且斜率不为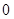 的直线交椭圆
的直线交椭圆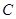 于
于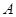 ,
,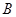 两点.试问
两点.试问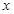 轴上是否存在定点
轴上是否存在定点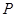 ,使
,使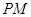 平分
平分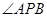 ?若存在,求出点
?若存在,求出点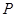 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.(Ⅰ)解:由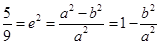 , 得
, 得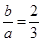 . ………2分
. ………2分
依题意△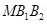 是等腰直角三角形,从而
是等腰直角三角形,从而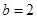 ,故
,故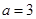 . …………4分
. …………4分
所以椭圆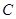 的方程是
的方程是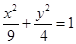 . ……5分
. ……5分
(Ⅱ)解:设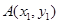 ,
,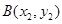 ,直线
,直线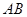 的方程为
的方程为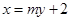 .
.
将直线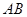 的方程与椭圆
的方程与椭圆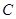 的方程联立,
的方程联立,
消去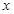 得
得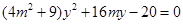 . ……7分
. ……7分
所以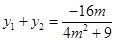 ,
,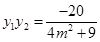 . ……8分
. ……8分
若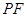 平分
平分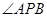 ,则直线
,则直线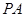 ,
,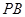 的倾斜角互补,
的倾斜角互补,
所以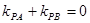 . …………9分
. …………9分
设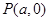 ,则有
,则有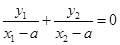 .
.
将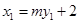 ,
,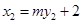 代入上式,
代入上式,
整理得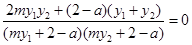 ,
,
所以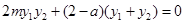 . ………………12分
. ………………12分
将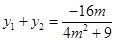 ,
,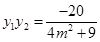 代入上式,
代入上式,
整理得 . ……………13分
. ……………13分
由于上式对任意实数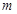 都成立,所以
都成立,所以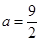 .
.
综上,存在定点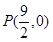 ,使
,使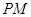 平分
平分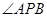 . …………14分
. …………14分
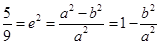 , 得
, 得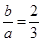 . ………2分
. ………2分依题意△
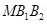 是等腰直角三角形,从而
是等腰直角三角形,从而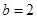 ,故
,故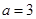 . …………4分
. …………4分所以椭圆
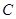 的方程是
的方程是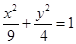 . ……5分
. ……5分(Ⅱ)解:设
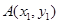 ,
,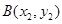 ,直线
,直线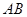 的方程为
的方程为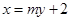 .
. 将直线
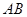 的方程与椭圆
的方程与椭圆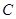 的方程联立,
的方程联立,消去
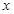 得
得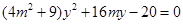 . ……7分
. ……7分所以
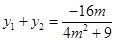 ,
,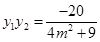 . ……8分
. ……8分若
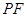 平分
平分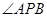 ,则直线
,则直线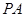 ,
,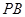 的倾斜角互补,
的倾斜角互补,所以
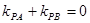 . …………9分
. …………9分设
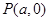 ,则有
,则有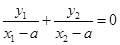 .
.将
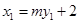 ,
,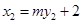 代入上式,
代入上式,整理得
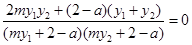 ,
,所以
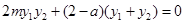 . ………………12分
. ………………12分将
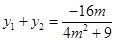 ,
,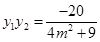 代入上式,
代入上式,整理得
 . ……………13分
. ……………13分由于上式对任意实数
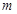 都成立,所以
都成立,所以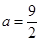 .
.综上,存在定点
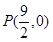 ,使
,使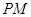 平分
平分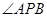 . …………14分
. …………14分略

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
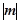
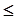 2,椭圆
2,椭圆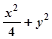 =1,p在椭圆上移动,求
=1,p在椭圆上移动,求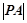 的最小值.
的最小值.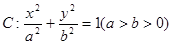 的离心率为
的离心率为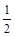 ,以原点为圆心,椭圆的短半轴为半径的圆与直线x-y+
,以原点为圆心,椭圆的短半轴为半径的圆与直线x-y+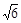 =0相切,过点P(4,0)的直线L与椭圆C相交于A、B两点.
=0相切,过点P(4,0)的直线L与椭圆C相交于A、B两点.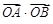 的取值范围.
的取值范围.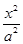 +
+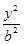 =1(a>b>0)上的点M (1,
=1(a>b>0)上的点M (1, 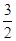 )到它的两焦点F1,F2的距离之和为4,A、B分别是它的左顶点和上顶点。
)到它的两焦点F1,F2的距离之和为4,A、B分别是它的左顶点和上顶点。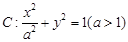 的上顶点为
的上顶点为 ,离心率为
,离心率为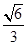 ,若不过点
,若不过点 与椭圆
与椭圆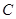 相交于
相交于 、
、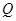 两点,且
两点,且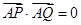 .
.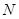 的坐标.
的坐标. 
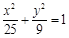 上一点P到它的一个焦点的距离等于3,那么点P到另一个焦点的距离等于 .
上一点P到它的一个焦点的距离等于3,那么点P到另一个焦点的距离等于 . 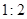 ,则此椭圆离心率的取值范围是( )
,则此椭圆离心率的取值范围是( )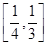
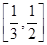
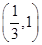
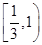
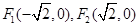 动点
动点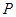 满足
满足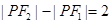 ,当点
,当点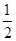 时,点
时,点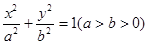 的左、右焦点分别为
的左、右焦点分别为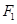 ,
,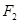 ,点
,点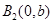 满足
满足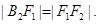
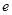 ;
;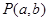 ,设直线
,设直线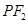 与椭圆C相交于A,B两点,且
与椭圆C相交于A,B两点,且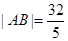 ,
,