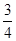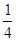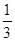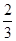题目内容
已知椭圆中心在原点,焦点在x轴上,离心率e=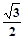 ,它与直线x+y+1=0交于P、Q两点,若OP⊥OQ,求椭圆方程。(O为原点)。
,它与直线x+y+1=0交于P、Q两点,若OP⊥OQ,求椭圆方程。(O为原点)。
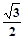 ,它与直线x+y+1=0交于P、Q两点,若OP⊥OQ,求椭圆方程。(O为原点)。
,它与直线x+y+1=0交于P、Q两点,若OP⊥OQ,求椭圆方程。(O为原点)。设椭圆方程为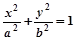 ,由
,由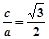 得
得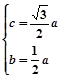
∴椭圆方程为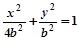 ,即x2+4y2=4b2
,即x2+4y2=4b2
设P(x1,y1),Q(x2,y2),则由OP⊥OQ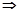 x1x2=-y1y2
x1x2=-y1y2
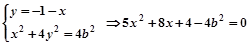
由△>0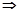 b2>
b2>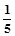 x1x2=
x1x2=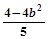 y1y2=(x1+1)(x2+1)=x1x2+x1+x2+1 =
y1y2=(x1+1)(x2+1)=x1x2+x1+x2+1 =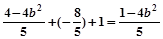
∴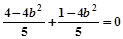 b2=
b2=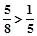 ∴椭圆方程为
∴椭圆方程为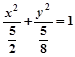
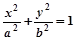 ,由
,由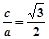 得
得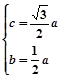
∴椭圆方程为
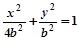 ,即x2+4y2=4b2
,即x2+4y2=4b2 设P(x1,y1),Q(x2,y2),则由OP⊥OQ
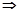 x1x2=-y1y2
x1x2=-y1y2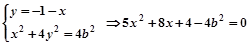
由△>0
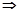 b2>
b2>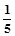 x1x2=
x1x2=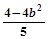 y1y2=(x1+1)(x2+1)=x1x2+x1+x2+1 =
y1y2=(x1+1)(x2+1)=x1x2+x1+x2+1 =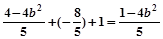
∴
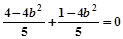 b2=
b2=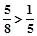 ∴椭圆方程为
∴椭圆方程为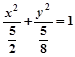
直线方程与椭圆方程联立,根据OP⊥OQ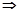 x1x2=-y1y2,求得椭圆方程为
x1x2=-y1y2,求得椭圆方程为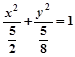
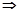 x1x2=-y1y2,求得椭圆方程为
x1x2=-y1y2,求得椭圆方程为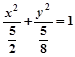

练习册系列答案
相关题目
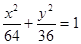 上一点P到它的一个焦点的距离等于4,那么点P到另一个焦点的距离等于_______.
上一点P到它的一个焦点的距离等于4,那么点P到另一个焦点的距离等于_______.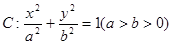 的离心率为
的离心率为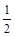 ,以原点为圆心,椭圆的短半轴为半径的圆与直线x-y+
,以原点为圆心,椭圆的短半轴为半径的圆与直线x-y+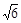 =0相切,过点P(4,0)的直线L与椭圆C相交于A、B两点.
=0相切,过点P(4,0)的直线L与椭圆C相交于A、B两点.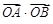 的取值范围.
的取值范围.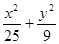 =1上任意一点,B为圆(x-1)2+y2=1上任意一点,则|AB|的最大值为________ 最小值为 ________
=1上任意一点,B为圆(x-1)2+y2=1上任意一点,则|AB|的最大值为________ 最小值为 ________ 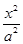 +
+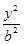 =1(a>b>0)上的点M (1,
=1(a>b>0)上的点M (1, 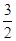 )到它的两焦点F1,F2的距离之和为4,A、B分别是它的左顶点和上顶点。
)到它的两焦点F1,F2的距离之和为4,A、B分别是它的左顶点和上顶点。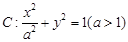 的上顶点为
的上顶点为 ,离心率为
,离心率为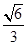 ,若不过点
,若不过点 与椭圆
与椭圆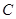 相交于
相交于 、
、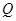 两点,且
两点,且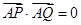 .
.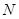 的坐标.
的坐标. 
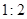 ,则此椭圆离心率的取值范围是( )
,则此椭圆离心率的取值范围是( )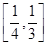
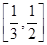
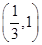
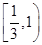
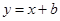 与椭圆
与椭圆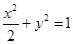 相交于
相交于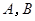 两个不同的点.
两个不同的点. 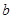 的取值范围;
的取值范围;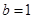 时,求
时,求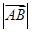
 有公共的焦点F1,F2,P是两曲线的一个交点,则
有公共的焦点F1,F2,P是两曲线的一个交点,则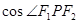 =( )
=( )