题目内容
3.下列参数方程中,与普通方程x2+y-1=0等价的参数方程是( )| A. | $\left\{{\begin{array}{l}{x=sinφ}\\{y={{cos}^2}φ}\end{array}}\right.$(φ为参数) | B. | $\left\{\begin{array}{l}{x=cosφ}\\{y=si{n}^{2}φ}\end{array}\right.$(φ为参数) | ||
| C. | $\left\{\begin{array}{l}{x=\sqrt{1-r}}\\{y=r}\end{array}\right.$(r为参数) | D. | $\left\{\begin{array}{l}{x=tanφ}\\{y=1-ta{n}^{2}φ}\end{array}\right.$(φ为参数) |
分析 利用同角三角函数基本关系式、三角函数的单调性与值域等可把A.B.C.D中的参数方程化为普通方程,同时注意检查未知数的取值范围即可判断出.
解答 解:A.普通方程x2+y-1=0中的y可以小于0,而$\left\{\begin{array}{l}{x=sinφ}\\{y=co{s}^{2}φ}\end{array}\right.$中的y≥0,因此不正确;
B.普通方程x2+y-1=0中的y可以小于0,而$\left\{\begin{array}{l}{x=cosφ}\\{y=si{n}^{2}φ}\end{array}\right.$中的y≥0,因此不正确;
C.x=$\sqrt{1-t}$≥0,而方程x2+y-1=0的x可以小于0,因此不正确;
D.$\left\{\begin{array}{l}{x=tanφ}\\{y=1-ta{n}^{2}φ}\end{array}\right.$化为y+x2=1,且x,y中的取值范围一致,因此正确.
故选:D.
点评 本题考查了参数方程的化简、同角三角函数基本关系式、三角函数的单调性与值域,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
2.已知函数f(x)=|lnx|-k有两个不同的零点a,b,则代数式|$\frac{{a}^{2}+{b}^{2}+2}{a-b}$|的最小值是( )
| A. | 8$\sqrt{2}$ | B. | 8 | C. | 4$\sqrt{2}$ | D. | 4 |
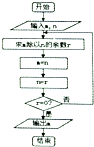 程序框图如图所示,若输入m,n的值分别为30,18,则程序框图中最后输出的m值等于6.
程序框图如图所示,若输入m,n的值分别为30,18,则程序框图中最后输出的m值等于6.