题目内容
2.已知函数f(x)=|lnx|-k有两个不同的零点a,b,则代数式|$\frac{{a}^{2}+{b}^{2}+2}{a-b}$|的最小值是( )| A. | 8$\sqrt{2}$ | B. | 8 | C. | 4$\sqrt{2}$ | D. | 4 |
分析 令f(x)=0,求出方程的两个根,代入代数式,结合基本不等式的性质,从而得到答案.
解答 解:令f(x)=|lnx|-k=0,则lnx=±k,
∴x=e±k,不妨设b=e-k,a=ek,
∴|$\frac{{a}^{2}+{b}^{2}+2}{a-b}$|=$|\frac{{e}^{2k}{+e}^{-2k}-2+4}{{e}^{k}{-e}^{-k}}|$
=|$\frac{{{(e}^{k}{-e}^{-k})}^{2}+4}{{e}^{k}{-e}^{-k}}$|=|(ek-e-k)+$\frac{4}{{e}^{k}{-e}^{-k}}$|
≥2$\sqrt{4}$=4,
当且仅当(ek-e-k)2=4,即k=${e}^{1+\sqrt{3}}$时“=”成立,
故选:D.
点评 本题考查了函数的零点问题,考查基本不等式的性质,是一道基础题.

练习册系列答案
 快乐5加2金卷系列答案
快乐5加2金卷系列答案
相关题目
12.设集合A={1,2,3},B={2,3,4},C⊆A∩B,则集合C可能是( )
| A. | {1,2} | B. | {1,3} | C. | {2,3} | D. | {2,4} |
17.执行如图所示的程序框图,若输入n的值为2,则输出s的值是( )
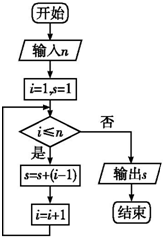

| A. | 1 | B. | 2 | C. | 4 | D. | 7 |
3.下列参数方程中,与普通方程x2+y-1=0等价的参数方程是( )
| A. | $\left\{{\begin{array}{l}{x=sinφ}\\{y={{cos}^2}φ}\end{array}}\right.$(φ为参数) | B. | $\left\{\begin{array}{l}{x=cosφ}\\{y=si{n}^{2}φ}\end{array}\right.$(φ为参数) | ||
| C. | $\left\{\begin{array}{l}{x=\sqrt{1-r}}\\{y=r}\end{array}\right.$(r为参数) | D. | $\left\{\begin{array}{l}{x=tanφ}\\{y=1-ta{n}^{2}φ}\end{array}\right.$(φ为参数) |
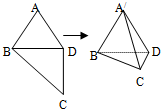 如图所示,在四边形ABCD中,AB=AD=CD=1,BD=$\sqrt{2}$,BD⊥CD,将四边形ABCD沿对角线BD折成四面体A′-BCD,使平面A′BD⊥平面BCD,则下列结论正确的是(2)(4).
如图所示,在四边形ABCD中,AB=AD=CD=1,BD=$\sqrt{2}$,BD⊥CD,将四边形ABCD沿对角线BD折成四面体A′-BCD,使平面A′BD⊥平面BCD,则下列结论正确的是(2)(4).