题目内容
已知:ΔACB为等腰直角三角形,∠ACB=900延长BA至E,延长AB至F,∠ECF=1350 求证:ΔEAC∽ΔCBF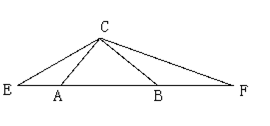

证明见解析
本试题主要是考查了平面几何中相似三角形的证明的求解。利用已知中ΔACB为等腰直角三角形,∠ACB=900延长BA至E,延长AB至F,∠ECF=1350 ,结合相似三角形的判定定理得到结论。
证明:∵AB=AC∴∠ABC=∠ACB,
∴∠BCF=∠ACE,
∵∠ECF=1350
∴△CBF∽△EAC
证明:∵AB=AC∴∠ABC=∠ACB,
∴∠BCF=∠ACE,
∵∠ECF=1350
∴△CBF∽△EAC

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
 内接于⊙
内接于⊙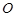 ,
, 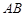 是⊙
是⊙ 是过点
是过点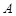 的直线, 且
的直线, 且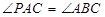 .
.
 交
交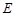 ,
,  ,
,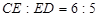 ,
,  , 求
, 求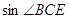 .
.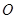 的半径OB垂直于直径AC,
的半径OB垂直于直径AC,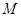 为AO上一点,
为AO上一点, 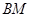 的延长线交⊙
的延长线交⊙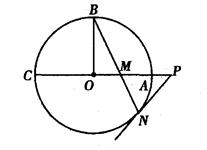
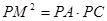 ;
;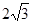 ,OA=
,OA=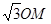 ,求
,求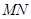 的长.
的长.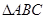 的外接圆的圆心为
的外接圆的圆心为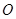 ,
,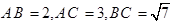 , 则
, 则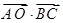 等于( )
等于( )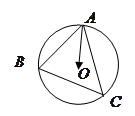
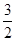
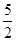
 与曲线
与曲线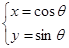
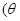 为参数,且
为参数,且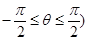 有两个不同的交点,则实数
有两个不同的交点,则实数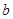 的取值范围是__________.
的取值范围是__________.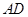 是
是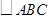 的高,
的高,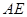 是
是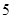 ,
,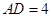 ,
,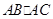 的值。
的值。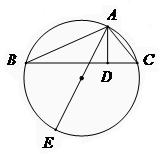
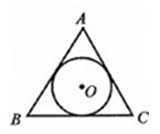
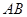 是⊙
是⊙ 的直径,
的直径,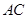 是⊙
是⊙ 的平分线
的平分线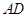 交⊙
交⊙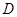 ,过点
,过点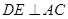 交
交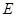 ,
,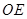 交
交 .若
.若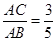 ,则
,则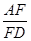 的值为 .
的值为 .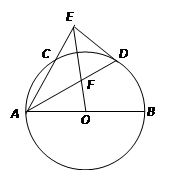
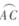 上的点(不与点A、C重合),延长BD至E,延长交BC的延长线于F .
上的点(不与点A、C重合),延长BD至E,延长交BC的延长线于F .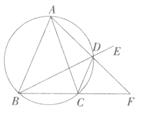
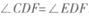 ;
;