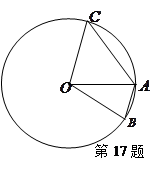题目内容
如图, ,
, 分别为
分别为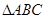 的边
的边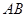 ,
,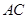 上的点,且不与
上的点,且不与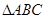 的顶点重合。已知
的顶点重合。已知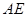 的长为
的长为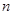 ,
,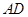 ,
,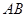 的长是关于
的长是关于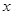 的方程x2-14x+mn=0的两个根。
的方程x2-14x+mn=0的两个根。
(Ⅰ)证明: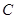 ,
,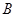 ,
,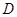 ,
,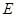 四点共圆;
四点共圆;
(Ⅱ)若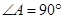 ,且
,且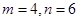 ,求
,求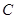 ,
,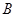 ,
,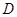 ,
,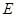 所在圆的半径。
所在圆的半径。
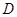 ,
,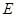 分别为
分别为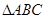 的边
的边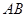 ,
,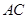 上的点,且不与
上的点,且不与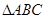 的顶点重合。已知
的顶点重合。已知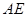 的长为
的长为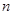 ,
,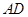 ,
,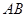 的长是关于
的长是关于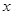 的方程x2-14x+mn=0的两个根。
的方程x2-14x+mn=0的两个根。(Ⅰ)证明:
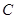 ,
,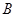 ,
,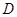 ,
,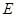 四点共圆;
四点共圆;(Ⅱ)若
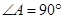 ,且
,且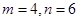 ,求
,求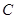 ,
,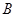 ,
,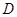 ,
,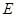 所在圆的半径。
所在圆的半径。
(1)略 (2)5

(I)利用四点共圆的判定定理探求成立条件即可证明;(Ⅱ)利用圆的知识确定圆心,然后求出半径即可。
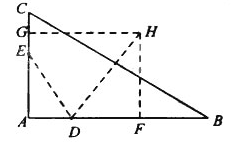
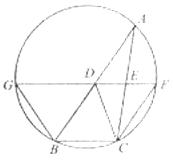
(I)连接DE,根据题意在△ADE和△ACB中, AD×AB=mn=AE×AC, 即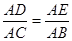 .又∠DAE=∠CAB,从而△ADE∽△ACB 因此∠ADE=∠ACB , 所以C,B,D,E四点共圆。
.又∠DAE=∠CAB,从而△ADE∽△ACB 因此∠ADE=∠ACB , 所以C,B,D,E四点共圆。
(Ⅱ)m="4," n=6时,方程x2-14x+mn=0的两根为x1=2,x2=12.故 AD=2,AB=12.取CE的中点G,DB的中点F,分别过G,F作AC,AB的垂线,两垂线相交于H点,连接DH.因为C,B,D,E四点共圆,所以C,B,D,E四点所在圆的圆心为H,半径为DH.由于∠A=900,故GH∥AB, HF∥AC. HF=AG=5,DF=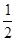 (12-2)=5.故C,B,D,E四点所在圆的半径为5
(12-2)=5.故C,B,D,E四点所在圆的半径为5
(I)连接DE,根据题意在△ADE和△ACB中, AD×AB=mn=AE×AC, 即
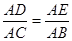 .又∠DAE=∠CAB,从而△ADE∽△ACB 因此∠ADE=∠ACB , 所以C,B,D,E四点共圆。
.又∠DAE=∠CAB,从而△ADE∽△ACB 因此∠ADE=∠ACB , 所以C,B,D,E四点共圆。(Ⅱ)m="4," n=6时,方程x2-14x+mn=0的两根为x1=2,x2=12.故 AD=2,AB=12.取CE的中点G,DB的中点F,分别过G,F作AC,AB的垂线,两垂线相交于H点,连接DH.因为C,B,D,E四点共圆,所以C,B,D,E四点所在圆的圆心为H,半径为DH.由于∠A=900,故GH∥AB, HF∥AC. HF=AG=5,DF=
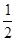 (12-2)=5.故C,B,D,E四点所在圆的半径为5
(12-2)=5.故C,B,D,E四点所在圆的半径为5


练习册系列答案
相关题目
 分别为
分别为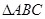 边
边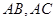 的中点,直线
的中点,直线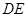 交
交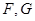 两点,若
两点,若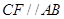 ,证明:
,证明: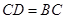 ;
;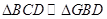
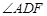 的度数;
的度数;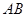 和
和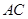 是圆的两条弦,过点
是圆的两条弦,过点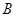 作圆的切线与
作圆的切线与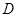 .过点
.过点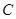 作
作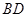 的平行线与圆交于点
的平行线与圆交于点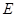 ,与
,与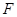 ,
,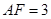 ,
,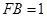 ,
,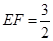 ,则线段
,则线段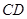 的长为 .
的长为 .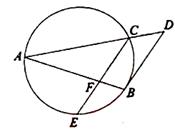
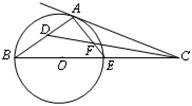
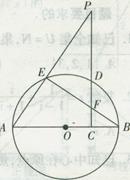
 以AB为直径的⊙O交AC于D,点E为BC的中点,连接DE、AE, AE交⊙O于点F
以AB为直径的⊙O交AC于D,点E为BC的中点,连接DE、AE, AE交⊙O于点F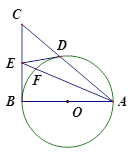
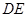 是⊙O的切线;
是⊙O的切线;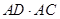 的值.
的值.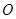 的直径,P为圆
的直径,P为圆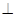 AB于C,交圆
AB于C,交圆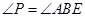 ;(Ⅱ)求证:
;(Ⅱ)求证: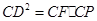
 中,点
中,点 到两点
到两点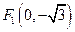 、
、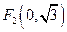 的距离之和等于4,设点
的距离之和等于4,设点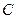 ,直线
,直线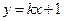 与曲线
与曲线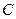 交于
交于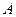 、
、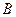 两点.
两点.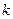 =1,求
=1,求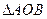 的面积
的面积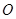 为△
为△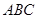 的外心,
的外心,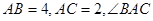 为钝角,
为钝角, 是边
是边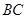 的中点,则
的中点,则 的值 ( ).
的值 ( ).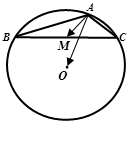
 的半径为
的半径为 ,点
,点 是⊙
是⊙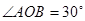 ,
,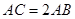 ,则
,则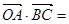 _____________.
_____________.