题目内容
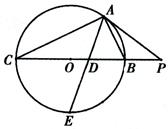
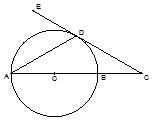
如图,C点在圆O直径BE的延长线上,CA切圆O于A点,∠ACB平分线DC交AE于点F,交AB于D点.
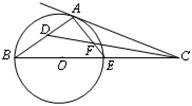
(I)求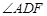 的度数;
的度数;
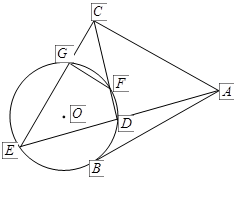
(II)若AB=AC,求AC:BC.

(I)求
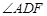 的度数;
的度数;(II)若AB=AC,求AC:BC.
(I) (II)
(II)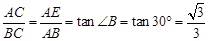
 (II)
(II)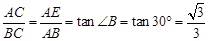
本试题主要是考查了圆内的性质和三角形的相似的综合运用。
(1)利用角平分线的定义和直径所对的圆周角为直角,结合分析得到所求的角。
(2)根据第一问的结论,分析三角形ACE相似于三角形ABC,然后得到线段的比例
关系式,结合直角三角形得到结论
解:(I)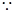 AC为圆O的切线,∴
AC为圆O的切线,∴ 又知DC是
又知DC是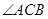 的平分线, ∴
的平分线, ∴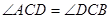 ∴
∴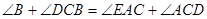 即
即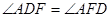 又因为BE为圆O的直径, ∴
又因为BE为圆O的直径, ∴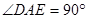 ∴
∴ …… 4分
…… 4分
(II)
 ,
, ,∴
,∴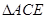 ∽
∽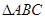 ∴
∴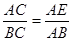 … 6分
… 6分
又 AB="AC," ∴
AB="AC," ∴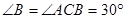 , ……………… 8分
, ……………… 8分
∴在RT△ABE中,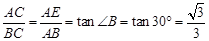
(1)利用角平分线的定义和直径所对的圆周角为直角,结合分析得到所求的角。
(2)根据第一问的结论,分析三角形ACE相似于三角形ABC,然后得到线段的比例
关系式,结合直角三角形得到结论
解:(I)
 AC为圆O的切线,∴
AC为圆O的切线,∴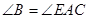 又知DC是
又知DC是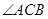 的平分线, ∴
的平分线, ∴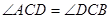 ∴
∴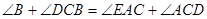 即
即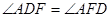 又因为BE为圆O的直径, ∴
又因为BE为圆O的直径, ∴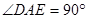 ∴
∴ …… 4分
…… 4分(II)
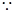
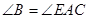 ,
,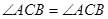 ,∴
,∴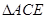 ∽
∽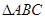 ∴
∴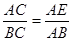 … 6分
… 6分又
 AB="AC," ∴
AB="AC," ∴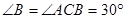 , ……………… 8分
, ……………… 8分∴在RT△ABE中,

练习册系列答案
相关题目
 是⊙
是⊙ 的一条切线,切点为
的一条切线,切点为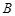 ,
,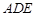 ,
, ,
, 都是⊙
都是⊙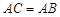 .
.
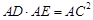 ;
;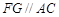 .
.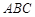 内接于⊙
内接于⊙ ,
,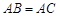 ,直线
,直线 切⊙
切⊙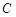 ,弦
,弦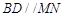 ,
,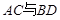 相交于点
相交于点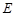 .
.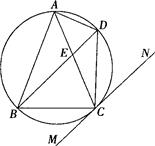
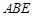 ≌△
≌△ ;
;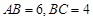 ,求
,求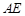 长.
长.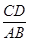 等于 .
等于 .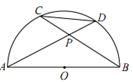
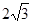 若
若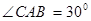 ,则圆O的直径AB等于( )
,则圆O的直径AB等于( )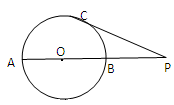 .
. ="6" cm,
="6" cm, 是
是 ,连接
,连接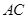 , 若
, 若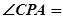 30°,PB的长为( )cm.
30°,PB的长为( )cm.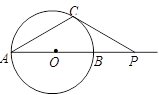
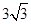
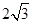
 是⊙
是⊙ 的直径,直线
的直径,直线 切⊙
切⊙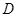 ,且与
,且与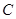 ,若
,若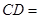
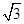 ,
,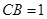 ,则
,则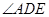 = .
= .
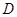 ,
,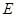 分别为
分别为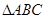 的边
的边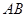 ,
,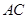 上的点,且不与
上的点,且不与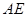 的长为
的长为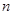 ,
,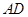 ,
,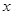 的方程x2-14x+mn=0的两个根。
的方程x2-14x+mn=0的两个根。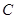 ,
,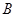 ,
,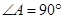 ,且
,且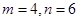 ,求
,求
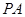 为⊙
为⊙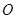 的切线,
的切线, 为切点,
为切点,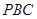 是
是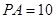 ,
,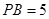 ,
,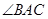 的平分
的平分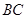 和⊙
和⊙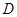 和
和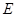 .
.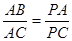 ;
;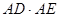 的值.
的值.